The Kau Particle
- Kalle Lintinen
- Nov 10, 2024
- 3 min read
Mathematics is a curious thing. You can look at the same thing, but when you change the angle of viewing, what you see can change radically. Instances of this are Laplace transforms and Fourier transforms, tools that us chemists need in the equipment and instruments that we use, but which we don’t necessarily need understand deeply ourselves: the computers do the transformations for us.
The reason why I talk about transformations is that the closer I get to the mathematically precise description of reflection of elementary particles of energy, the more geometric tools ‘pop up’ just from looking at the problem. This time I had started building my unit cell of reflection from one angle and had reached a point where I couldn’t proceed. So, I changed the angle of view for the Amazing Graze and beyond.
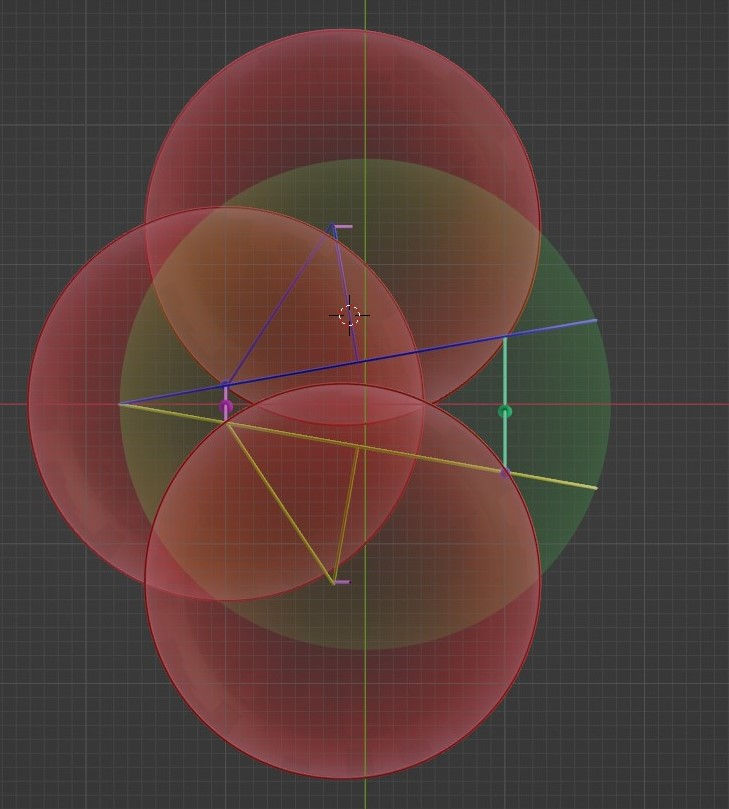
However, after my last post, I realized that I had spent the usefulness of the alternative point of view and would need to apply the geometry to the original perspective of the unit cell of reflection. So, back to the unit cell of reflection it is. When I applied the Sphere of Reflection to the unit cell of reflection, I was able to draw the projections below. Because I changed the center of the structure to the unit cell of reflection, the old projections don’t apply.
In the y-z projection you can best see the two different grazing paths at the center: the purple one, which is connected to the neighboring spheres of reflection and the turquoise one, whose spheres of reflection aren’t shown. This means that beginning and end point of reflection with the purple path is separated by three spheres of reflection and in the turquoise path, the separation is five spheres of reflection. This is something that I need to study in a bit more detail.

In the x-z projection you can actually see the reflection. The purple paths above and below are more or less the same as the purple path in the center, but different to the turquoise path. Again, I know this intuitively, but I can’t explain this any better until I’ve studied the idea more.

And in the x-y projection you can clearly see how the spheres of reflection are levered from a joint plane. Or at least you could, if I was able to explain the mechanism a bit better.
And as always, here is the rotating 3D shape:
So, is this the final solution? Is reflection perfectly explained? If you look at the projections closely, you might see that the shapes don’t fit perfectly yet. For a while I thought that I wouldn’t post anything until I found the perfect fit. But then I realized that I usually learn the best when I try to explain my ideas in these posts. And I wasn’t wrong. Just trying to explain myself, I’ve made significant progress.
After all I’ve said in this post, you might ask what is the title all about? What is the kau particle? I’ve been pondering for a while about the name that I’ve given to the elementary particle of energy: the dot. While dot is a simple name, I fear that it can too easily be confused with the punctuation mark. Last Friday I had an epiphany: the name should follow the quirky convention of naming subatomic particles. I’ve talked before about the spherical cow, and the phrase:
"I have the solution, but it works only in the case of spherical cows in a vacuum."
Well, the above statement describes my particle perfectly. It is spherical and moves in a vacuum. However, I don’t want to call it a cow-particle, because that would be a bit too much. But as there is a tau particle, the name kau particle would fit the naming convention perfectly. As most of you know, the phonetically cow is pronounced /kaʊ/, which is for a Finn is pretty much identical to kau.




Comments