Perfecting Asymmetry
- Kalle Lintinen
- Nov 5, 2024
- 3 min read
If you’ve been reading my posts on my quest to explain the Theory of Everything by the reflection of elementary particles of energy (dots), you might notice the theme of perfectionism cropping up time and time again. The reason for this is quite simple: mathematical proof (as far as I understand) needs to be perfect. If it’s not perfect, it’s not a proof at all.
The only problem with above is that actually getting to the proof can require leaps of faith. Or “then a miracle occurs” in the holes of the theory. To some extent these MacGyvered fixes hold the theory in rough shape, but they can’t be left in the final theory. Basically, these fixes look at a complex problem and solve the biggest issues, leaving the small issues unmended. But if these smaller issues aren’t addressed at some point, the theory will collapse like a house of cards at some point.
So, this is where I left after my last post. I had a nearly perfect theory of reflection. Except the red rings of reflection looked just a bit wonky. This wonkiness wasn’t even that pronounced. The bigger problem was that the way I had drawn the reflection model, the red reflection rings should be perfectly vertical, while the yellow paths of the dots were tilted semi-horizontal vectors. But because by definition, the red reflection rings should be orthogonal to the yellow path vectors, there was something off in the model. And this was the lack of asymmetry! I’ve been toying around with asymmetry in my posts for a long time, but still haven’t figured it out properly. Or at least hadn’t, until now. Or I sort of had, but forgot to carry the knowledge when trying to tackle a new problem.
Perhaps the best way to describe this asymmetry is to show the y-z projection with red reflection rings:
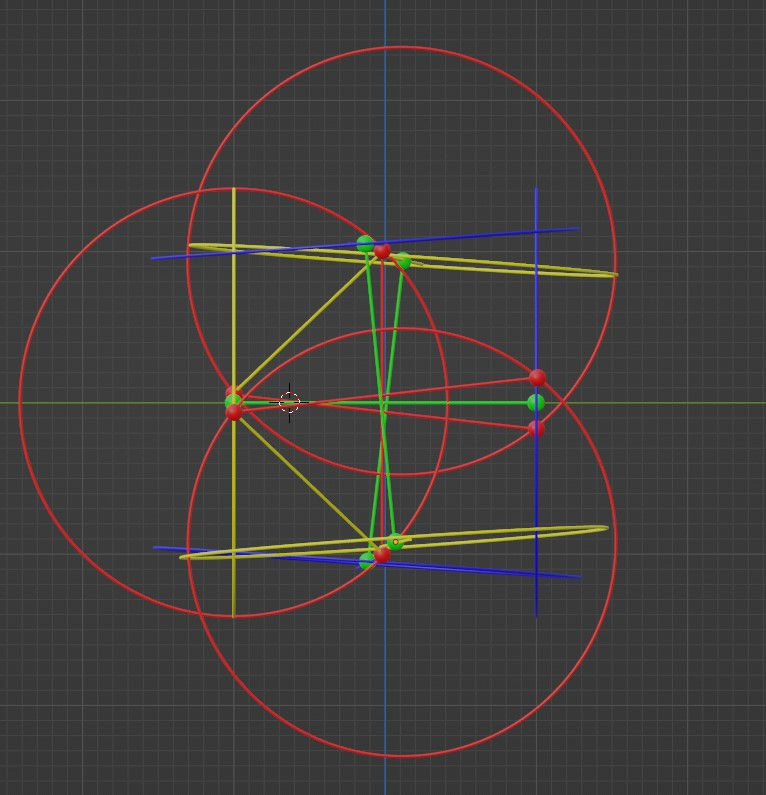
If you look closely, the red tilted horizontal vectors that show the distance between neighboring dots at the instance of reflection are lopsided. That is, their crossing point in this projection is closer to the left side than to the right. This means that the yellow dot on the left moves in a more horizontal path than the blue dot on the right.
The whole paths are better visible in the y-z projection:

The blue path is much more tilted from the horizon than the yellow. This means that the dots in the middle of the yellow ellipses (projections of yellow rings) are furthest away from the (vertical) z axis, with the dots at the end of the yellow vector being next furthest away, the dots at the end of the blue vector being the second closest to the z axis, and finally the dots in the middle of the blue ellipses are the closest to the z axis. But I’m not yet sure whether or not these dots should be aligned on the same line in the projection. Because they’re not on the same line in the y-z projection.
And as I say all of this, I have a feeling that the x-y projection is probably the key to understanding the shape:
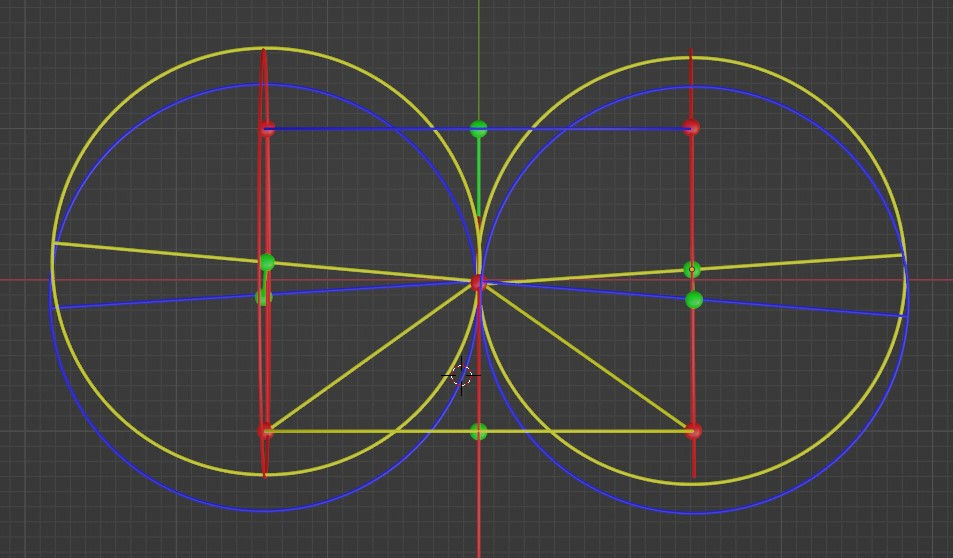
But as I was about to explain the basis of this feeling, I realized that I couldn’t. Rather, I see a pattern emerging, but the details are still very fuzzy.
So, this is what I’ll be working on next. If my intuition is correct, there’s a chance that it will be the final solution. And if it isn’t, I’ll just continue toiling away…




Comments