Sphere of Reflection
- Kalle Lintinen
- Oct 23, 2024
- 3 min read
Today’s post might come too early, because I’m going to talk about a concept that isn’t yet fully clear inside my own head. But the reason I want to write a post about it is that I’ve noticed that the best way to teach yourself is to teach others. Or “Docendo discimus”, to be very fancy.
This new idea arose when I tried to apply the Twist and Bend -model of reflection to the Unit Cell of Reflection. First of all, I realized that the Twist and Bend -model had to be tweaked a bit. Basically, the idea of the inward bending of the already twisted shape was on the right tracks, but I realized that the inward bending should not be from the same side, but from the opposite ends of the shape. This will probably sound incomprehensible to you, dear readers, but I say this just to explain why the model I am presenting today looks a bit different from before. I’ll have to figure out the details myself before I can explain them to you. I’m still partly relying on intuition.
But the more important idea that I realized is that at the point of reflection, the four elementary units of energy (dots) involved in the reflection event are located on the surface of a sphere with a radius slightly higher than half the flight path of a dot between two reflections.
If I had planned the angles of reflection of my shapes properly, the two shapes would fit together. However, because I had the above realization of the sphere of reflection just now, my current shapes are completely mismatched. Nevertheless, I’ll try to use what I have to convey the idea.
This y-z projection (now with opposite bends), with the unit cell of reflection overlaid shows the rough idea of how the sphere of reflection should work (but doesn’t yet). The horizontal red cylinder connecting the two red central dots, should in fact be tilted slightly to the left, as shown in the Reflection or Not? -post. The dots should also be on the same plane as the two vertically neighboring dots in the Twist and Bend -shape.

And these aren’t even all of the requirements that the combination of these two shapes need to meet. Suffice it to say, I know what my shape should look like, but making the required changes will take some time.
And here is the x-y projection of the combined shape. Again, the four dots on the left should be on one plane, as should the four dots on the right.
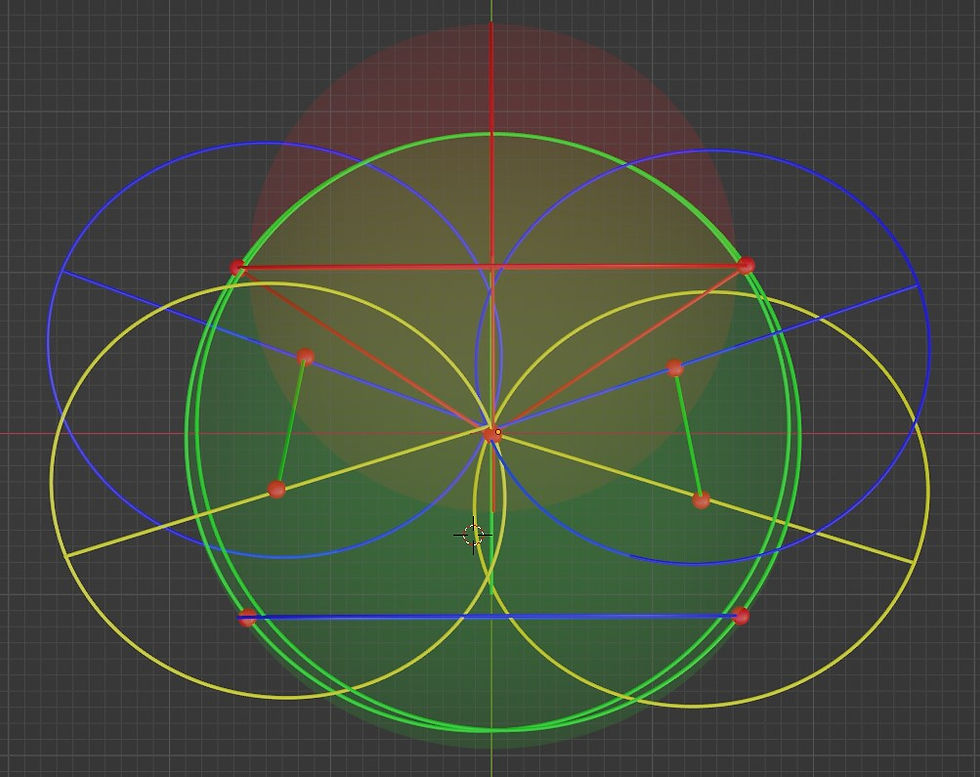
And finally, here is the x-z projection. Here the problem is that the two vectors drawn through the opposite neighboring dots on a plane should be perpendicular to each other and in this case they clearly aren’t yet.
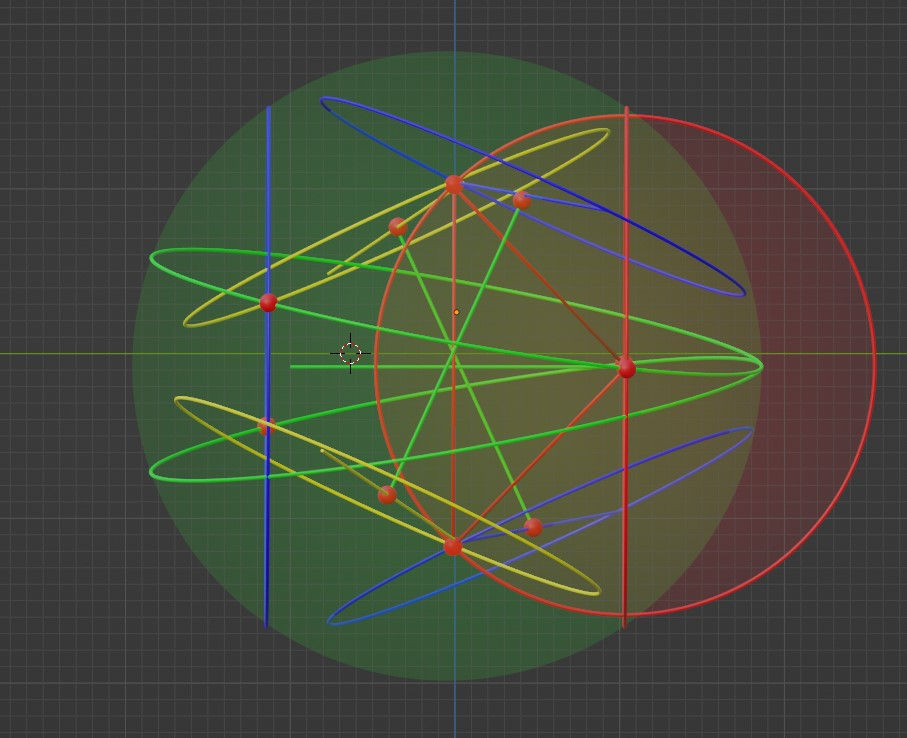
And this is what the above mess looks like as a rotating 3D model:
So, why am I showing something this incomplete? Because I believe strongly in the docendo discimus -model. And I think it’s better to be wrong and know it, than to be vague. In natural sciences there is a tendency to keep some of your hypotheses to yourself, if you’re not absolutely convinced about them yourself. However, the best way to find the faults in any hypothesis is to expose them to scrutiny.
As a matter of fact, the model above is a lesson in the sometimes-schizophrenic nature of discovery. At the same it shows qualitatively that all of the requirements for this complex set of reflections can be met in principle. However, it clearly has an element of “then a miracle occurs” left.
I just hope that my next post will be a cry of Eureka, instead of a whimper.




Comments