Twist and Bend
- Kalle Lintinen
- Oct 19, 2024
- 2 min read
In today’s post I introduce my first attempt at combining the two types of reflections I’ve presented in my post: the twisting reflection in the Amazing Graze -post and the bending reflection in the Curved Grazing -post. In the end, the solution seems quite elegant, but it nevertheless involved banging my head against the wall for a few hours before coming up with it.
Again, I’d be tempted to elaborate on all of the wrong attempts, but focusing on those would just be too confusing. Instead, I’ll just get to the final solution. That is, I took the basic model that I had presented in the Amazing Graze -post and bent the twisted shapes around the x-axis, as can be seen in this y-z projection:

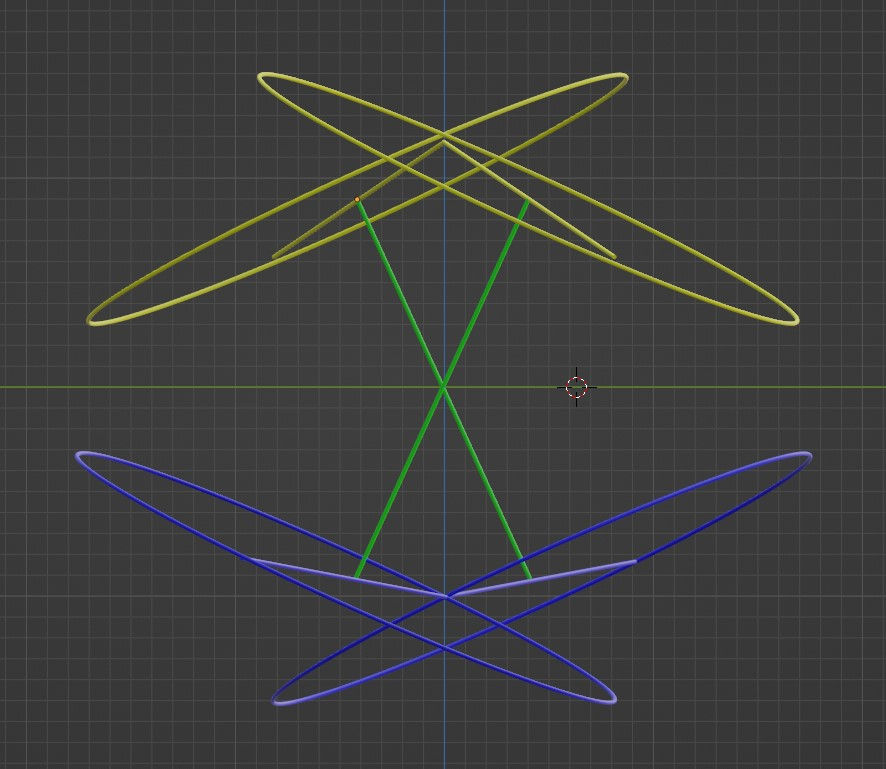
And just as I had predicted in the post, I moved the grazing rings below (drawn in blue this time) further from the vertical z-axis, so that the grazing points (marked with green cylinders) are no longer located at the midpoint of the (blue) grazing vectors.
Probably the best projection to see the asymmetry in this shape is the x-y projection:

And for full picture here is the x-z projection, where the bending has caused the projections of the grazing rings to have expanded from straight lines to thin ellipses:
And here is how the shape looks like when it’s rotating:
Personally, I think the difference between the pure twisting in the Amazin Graze -model becomes diminished in this rotating shape.
If this model is the final solution, I should be able to see this with the reflection equations based on this shape pretty soon. That is, if I don’t procrastinate and actually start working on it immediately.




Comments