I’ve been writing and rewriting today’s post so many times I’ve lost count. I started writing something, then realized I was wrong, and then started writing about that until I realized I was wrong again, until finally I realized that I hadn’t been that wrong in the first place: just a little bit. But instead of explaining what I had thought of before, I’ll just save you the trouble and get to the meat of today’s post. And that is: I have finally found to explain reflection with grazing rings.
I would like to wax lyrical about my misconceptions about the Reflection or not? post, but it’s easier to say that the general shape was correct but a lot of my musings about it was misguided. So, you can read the post as a reference, even though reading it can be a bit misleading.
So, not repeating all of the silly mistakes of before, how does one use grazing rings to describe reflection of elementary particles of energy (dots)? Honestly, the solution is so simple that I’m almost embarrassed that I didn’t see it immediately. In short, you take two pairs of grazing rings and tilt them in the opposite directions around a common axis and place them next to each other so that the neighboring rings touch, Like here in the y-z projection:
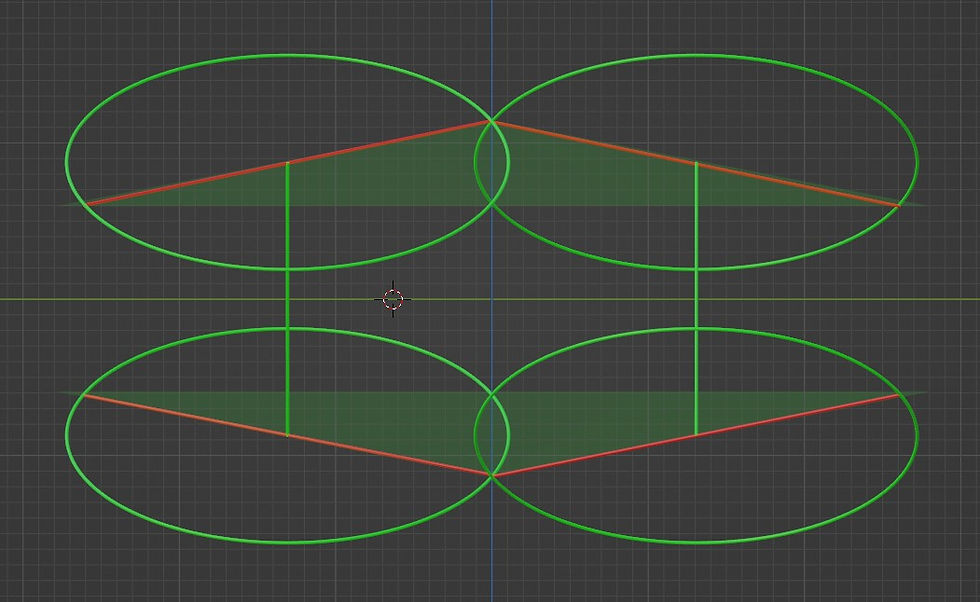
In just one projection the shape can look confusing. You can see the tilting much better in the x-z projection:
But there you can’t really see the red grazing vectors anymore.
On the other hand, the best way to see the non-reflected components of the grazing vectors is to look at the x-y projection:
And as always, here is the amazing grazing scheme rotating in 3D:
I’m almost at a loss for words how fast this solution emerged from the grazing ring -shape.
However, I think there must still be a couple of surprises left. The reason for this is that this kind of reflection doesn’t seem to be causing any overall bending of the trajectory of the dots. This seems to imply that the dots don’t necessarily graze at the halfway point of two reflections. But it can also mean something else, or I might be wrong about something else.
Whatever the case may be, I’m constantly finding interesting new things out. And as Richard Feynman said “There is a pleasure of finding things out”. And finally, sorry about the bad pun in the title...
Comments