In my last post I introduced a mathematical tool to describe reflection of elementary particles of energy (dots). I called this tool a tetracone of reflection, for the obvious reason that it describes reflection, and it is comprised of four cones. But I didn’t show how these tetracones are used in action. In today’s post I’ll attempt to do exactly this.
The below picture (y-z projection) isn’t really accurate, but rather a simplified explanation of the mechanism of reflection. On the left and right, you have two tetracones of reflection. The cylinders/vectors inside the tetracones are actually just the green cylinder from the center, shifted to the center of the dot that is being reflected. That is, the green cylinder in the center is the path of the blue and yellow dots that are being reflected.
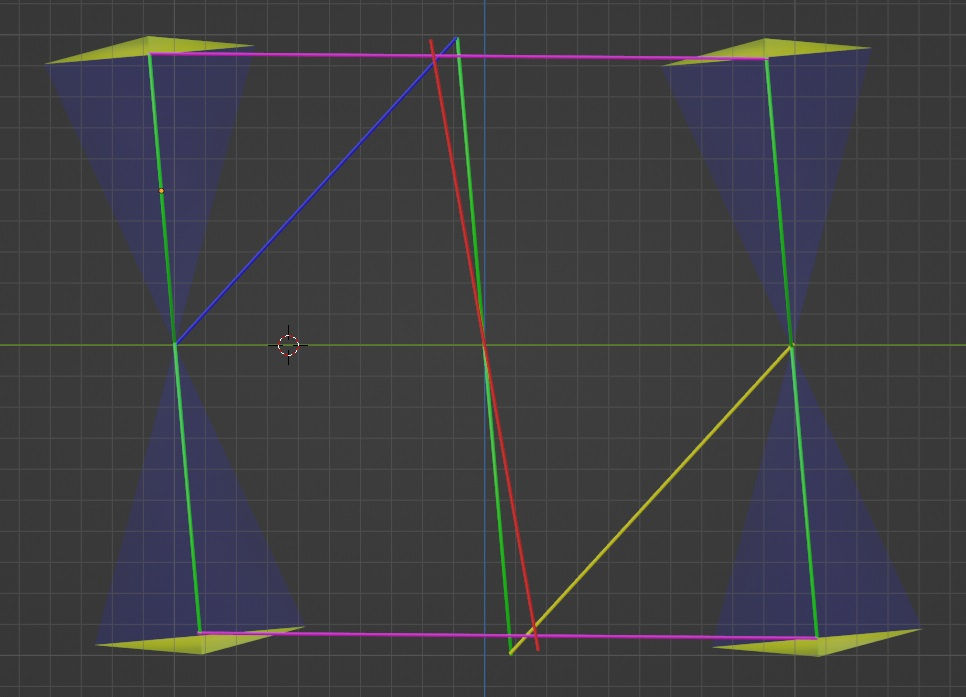
In this simplified y-z projection, one doesn’t see anything of the Reflection K. I.e. the K-shape is only properly visible in the x-z projection (I’ll show you in the next paragraph) and in a ‘compresses form’ in the x-y projection. However, if I was fully accurate, the cones would be slightly rotated inwards, so that the purple ‘grazing vector’ seen above and below would have a smaller length than the center-to-center distance of the two tetracones. This rotation would reveal a bit of the K-shape in this projection as well.
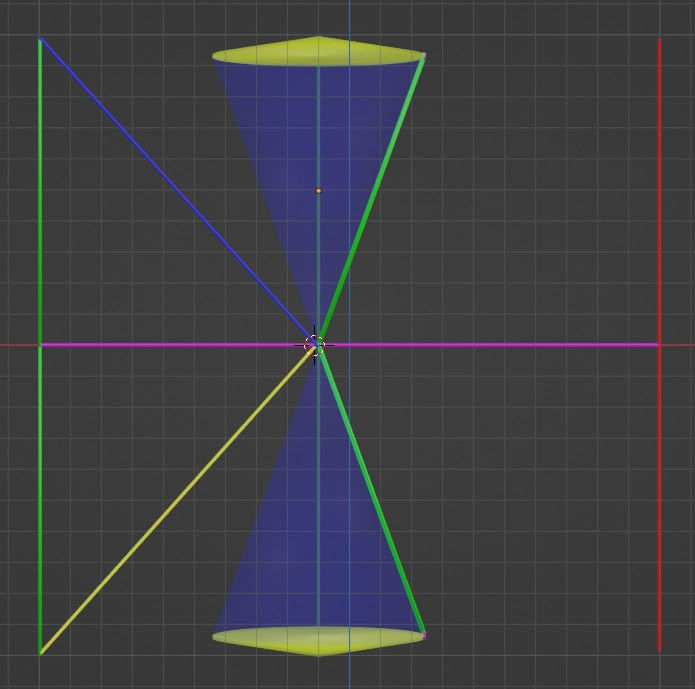
And as promised, in the x-z projection shows the Reflection K the best. In this projection you can see the red vector on the right side, all by itself. While the dots moving along the red vector grace with the dot moving along the green vector on the left at the center (marked by the purple horizontal vector), these dots are not involved in this reflection event. However, the vector on the right will ‘take part’ in the reflection event before and after the one shown her. And as noted in my previous posts, the blue and yellow diagonal vectors depict the blue-blue and yellow-yellow dot connections in the reflection events.
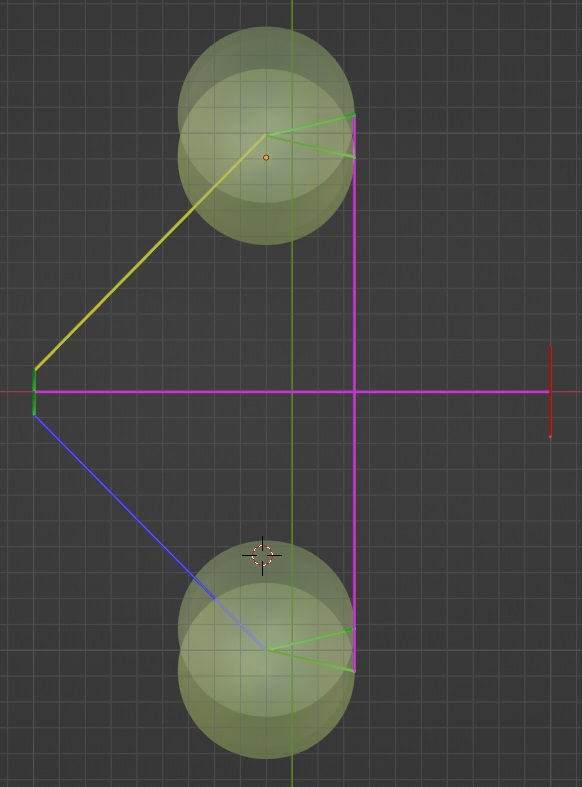
And last, but not the least projection is the x-y projection that the dots reflect from one rim to the next rim of the reflection tetracone. At least in this simplified model, the two purple reflection vectors appear to overlap.
And as always, this is what the model looks like when rotating:
In my previous post I was certain that because of the geometry of my reflection model, the neighboring dots must move in opposite directions. However, based on this reflection tetracone, I’m not as certain of it as I initially was. Based on the above model, the dots don’t seem to ‘care’ about the direction of movement of the dots, only about the geometry of the dots at the point of reflection. However, as my intuition about there being no curves seems to be right, my intuition about the opposite path might still be correct as well. I’ll just have to think about this further to form a solid opinion.
From the model above, you can see that it seems to be possible to combine the older model with this newer one, but this can’t be taken for granted. Only if the mathematics of the two models fit seamlessly, can I be confident that I haven’t painted myself into a corner. So this is my next task.
Commentaires