Opposite Arrows of Spacetime
- Kalle Lintinen
- Sep 15, 2024
- 3 min read
In my last post I presented the Reflection K, that shows the reflection of the center point of two elementary particles of energy (dots). I stated that the image showed the first concrete model of the actual reflection of dots and not just the approximate arrangement of dots along an orbital.
However, almost as soon as I’d finished the post, I started looking more closely at the image I had created, and especially this x-y projection:
There was something fishy about the projection and I said as much in the post: the nearly vertical vectors ending in tiny spheres that depict the centers of dots didn’t make sense reflection-wise. There seemed to be no way to make reflection with these large angles make sense. But I had my hopes that if I just reduced the angle, things would be sorted out.
But this didn’t happen. I managed to write the equations for the distance of the (vertical) y component from the x-axis. And when I reduced the angle, the blue dot in the top center was always farthest away from the x axis.
For an instant I thought that there must be something wrong with my model. And to some extent, yes there was. You see, I thought that the angle between the circular planes of reflection would always be (more or less) the same. But looking at the model, this assumption was untenable. Rather, reflection, if my intuition is correct, must lead to a conical spread, where the distance of the dot from the center grows linearly as a function of time.
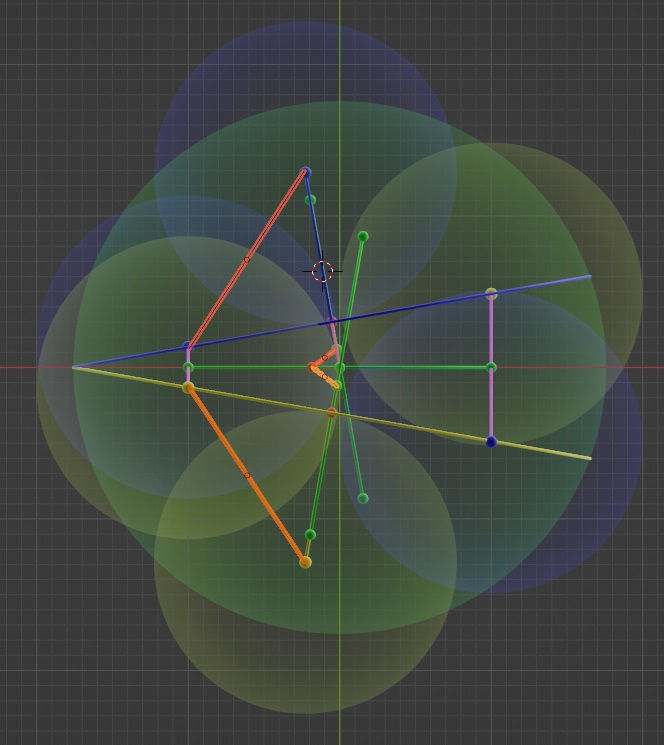
This means that if the neighboring dots were moving in the same direction, this reflection would lead to an uncontrolled spread of the dots, or an impossible infinite shape. Thus, it seems almost 100 % sure that neighboring dots cannot move in the same direction. Or more specifically if the neighboring dots move in the opposite direction, the sum distance of the neighboring dots from the center can be a constant. The exact mathematics of this requires more thought, but today I can illustrate the concept by showing the model from the Reflection K post with opposite arrows of spacetime.

The above model still has a few errors relating to the old model, because I haven’t changed the old geometry based on the new concept. But I have included the opposite arrows of spacetime to the shape. While the shape is rather complicated, you can see the Y-shapes describing reflections. On the left side you have an upside-down Y, with two red arrows and a blue cylinder. The top arrow is the arrow of approach. When the blue dot touches another blue dot, this contact is described with a blue cylinder, resulting in the conservation of the parallel motion of the two dots and the mirroring of the motion not parallel, along the plane defined by the two vectors: the arrow of approach and the cylinder of blue-blue connection. But because a) the model has a too large angles, and b) the distance from the center of the dots remains constant, the reflection seen in the model looks impossible.
However, if you look at the right side and the Y-shaped reflection of yellow dots, you might be able to see that this mirroring of the reflections allows the sums of the distance from the center to remain constant. Or at least you could, if I made the corrections based on today’s discovery.
And here is what the model looks like when rotating:
Next you might ask: “Does this really solve the problem of the growth of the cone of reflection?” It won’t by itself, but if you’ve read more of my posts, you might remember the saint Hannes knot. My intuition says that the cone grows from the smallest distance right after the reflection from the knot and gradually grows ever larger until the cone is reverted to its minimum radius at the point of reflection.
But all of this is extremely preliminary. I’m still trying to figure all of this out. However, this theory (or hypothesis) is so logical that I can’t imagine it not being correct. The pleasant thing is that this hypothesis is testable. It will produce equations of reflection that either make sense, or they won’t. If they make sense, the theory is more or less ready. And if they don’t, it’s back to the drawing board, once more.




Comments