The Reflection K
- Kalle Lintinen
- Sep 13, 2024
- 3 min read
In today’s post I reveal the first trigonometric description of reflection, based on the model I’ve been working on for these past weeks. In previous posts I’ve described the linear movement of elementary particles of energy (dots) from one circular plane of reflection to another. However, in these posts, I’ve just assumed that dots are reflected. These older models haven’t described reflection itself. However, I haven’t worried about this, as I’ve been confident that once the model is finished, reflection would be an emergent property of the shape.
And this is what has seemed to have happened. First, I added the same green perpendicular cylinders, describing the grazing spot of neighboring dots, to the front and back of the shape (above and below in the x-z projection below). Then I could connect the red dots not at the center of the rod to the green dot in the middle green rod. Then I also drew vectors between the blue and green dots that are in contact with each other. And there it was: a K-shape, with two diagonal cylinders describing the blue-blue and yellow-yellow dot connections, as well as two vertical cylinders at a slight angle to each other, describing the path before and after reflection. The important thing to understand is that the K-shape is a combination of (diagonal) space vectors and (almost vertical) spacetime vectors.
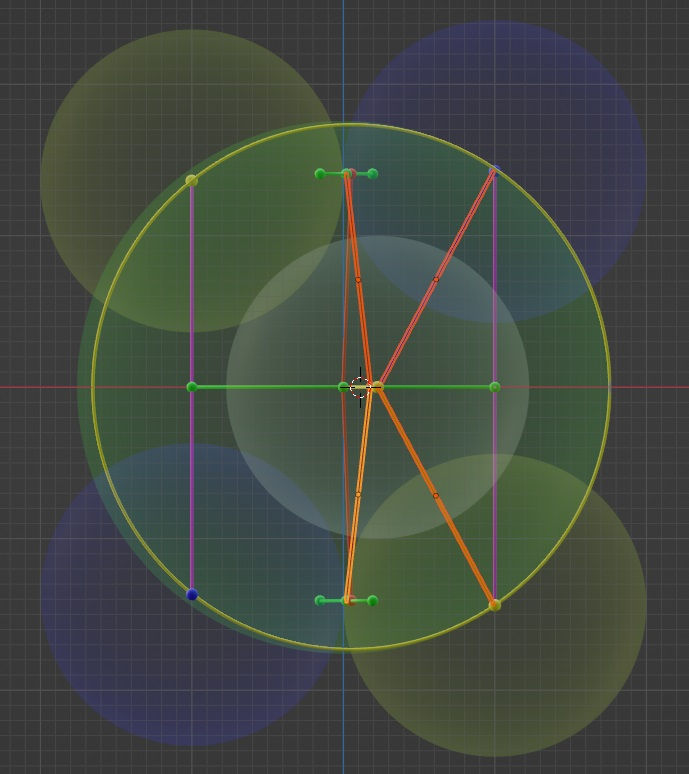
And this is the basis of the trigonometric proof of the Theory of Everything. Or more specifically, with this shape it should be possible to prove the Theory of Everything with trigonometry. The shape itself isn’t the proof just yet.
At this point you might be asking why I show screen captures from Blender instead of the 3D images that can be generated with Blender. The answer is quite simple in Blender you have the possibility of seeing your models as perfect 2D projections, where the third dimension is totally flattened. In all of the 3D viewing programs I know of there is no flattening function. And you can only see the precise geometry with projections.
So, what happens in the other two projections? Well, in the y-z projection below, it seems as if there’s almost no reflection between the two vectors connected to the origin (center).
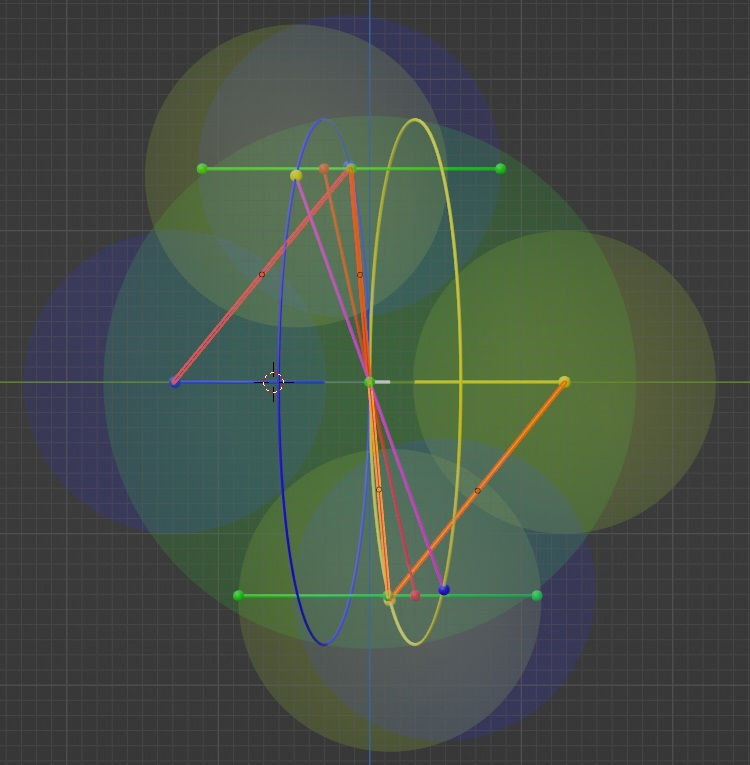
However, when one looks at the x-y projection below, one observes that there is indeed some reflection, but conversely no passing through the true origin. That is the path of the center of the two dots passes the point Δ,0,0, where Δ is the shift from the origin along the x axis, but where the path along the y-z projection truly passes the ‘pseudo-origin’ of 0,0, with the x-axis ignored.
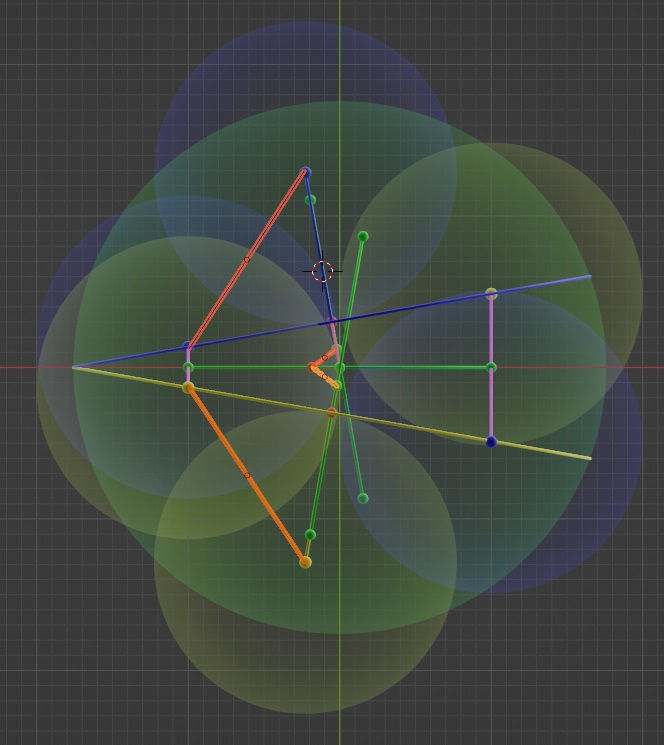
This means that there is two-dimensional plane along which the center of the pair of dots is reflected, as seen in 3D:
There is one thing that I intentionally didn’t include into this model. That is, the vector paths of the individual dots above the 2D plane of reflection. The reason is that with the large angle used in this model the reflection isn’t logical. In this model the dots are farthest from the plane at the instance of reflection, giving the impression that there would be an attractive force to the point of reflection. However, I think if reduce the angle between the two rings, the depicted reflection should become logical. But because the induvial reflections aren’t logical in the above image, I’ll ignore them until I can prove (or disprove) that my model is logical.




Comments