The Non-Crackpot Shape of Reflection
- Kalle Lintinen
- Oct 30, 2024
- 3 min read
I’ll start today’s post on my quest to explain the Theory of Everything with the reflection of elementary particles of energy (dots) with something different. I came across a very nice YouTube video on physics crackpots. It explains perfectly, how the world is full of retired engineers and other mathematically talented people who have become disillusioned with modern physics and have decided that everyone else is wrong (especially Newton and Einstein) and that they have figured out the ‘hidden truth’.
These people spend much of their time on different media ranting on about their ‘discoveries’ and flooding the mailboxes of physicists with their ‘verbal proofs’ that are extremely thin on mathematics.
While I don’t consider myself a crackpot, nor would they. So, what makes me so sure that I’m not one of these people who think they have solved the Theory of Everything, but actually have discovered bupkis? The short answer is, I cannot be sure until the mathematics makes sense. If after all these posts for over two years, I manage to show that my idea of reflection of elementary particles of energy is mathematically impossible, this would crumble the foundations of my theory and would show that I have feet of clay.
This is very much the reason why I haven’t sent incomplete versions of my theory to physicists. How could they know that I’m not one of the scores of crackpots who are mathematically talented, but lack the knowledge of modern physics? The only way to overcome this natural skepticism is to present mathematical proof of the theory. The interesting thing mentioned in the YouTube video on physics crackpots was that why don’t the crackpots never solve simple problems first, but always go immediately for the first prize. Well, I think what I’ve been doing these couple of months relating to the mathematical description of reflection would be the first instance of ‘going small’ to go big. The very small problem is how to describe a system where the only allowable interaction is the reflection of identical spheres moving at identical speed with no other fundamental interactions.
So, how am I doing? Well, from my perspective I’m doing extremely well, with new insights almost daily, or at least weekly even in slower times. But from the perspective of an outsider, things are not as straightforward. Yes, I seem to be doing a lot, but at the same time I don’t tend to show too many equations in my posts. So, what am I doing? I’m using a variant of the spherical cow, where I simplify the problem of reflection into a toy model. The model might not be correct but allows me to turn the idea into equations. Except most of the time I don’t even need the equations to see where the model needs revision.
And what does my spherical cow look like today? Here is the rotating 3D model of grazing rings twisted and bent in a way where all of the paths in a reflection event are presented and seem to make sense:
It’s more or less the shape from the Sphere of Reflection -post, but this time with the points of grazing again at the center of the grazing rings. This is best seen in the y-z projection:
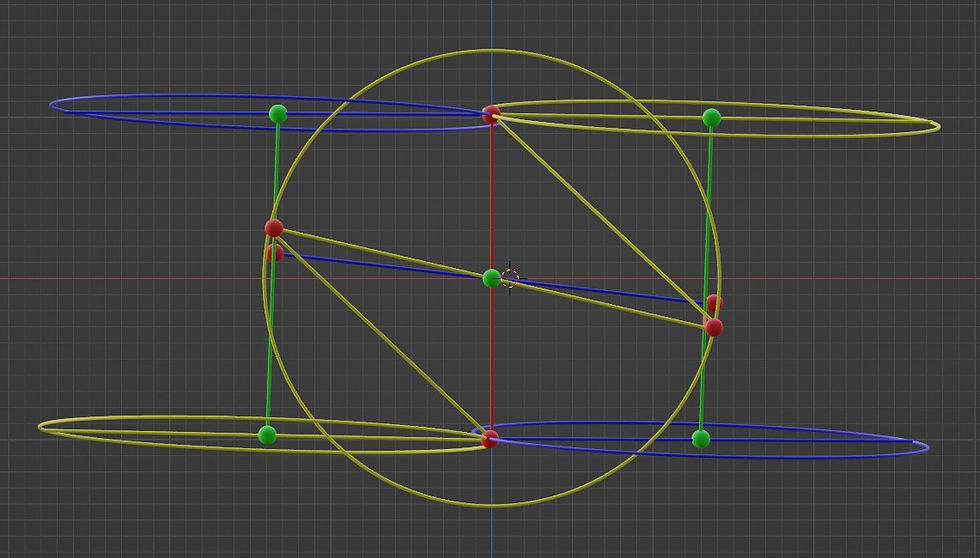
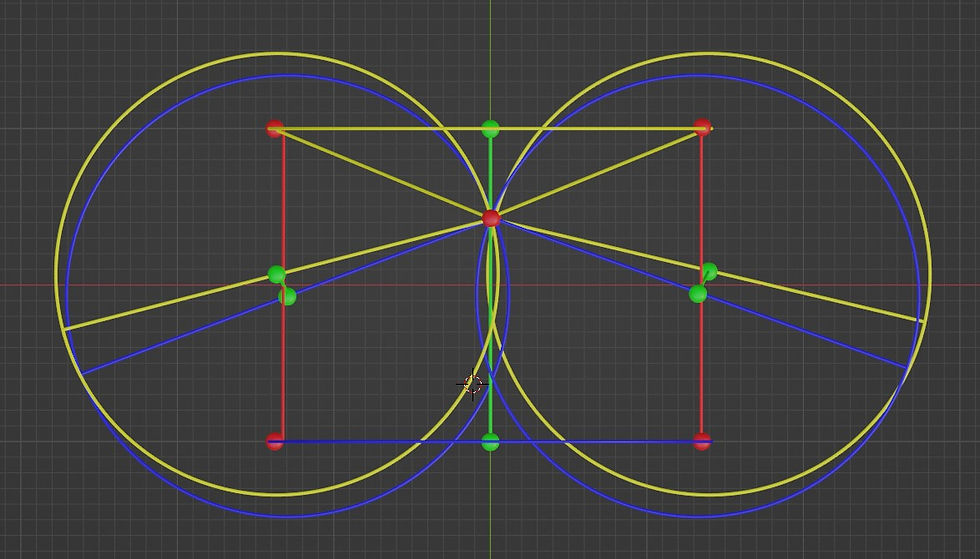
This new model seems to reverse the reflection from being along the y-z plane to being along the x-y -plane (at least mostly so), as seen in the x-y -projection:
And for completeness, here is the y-z projection:
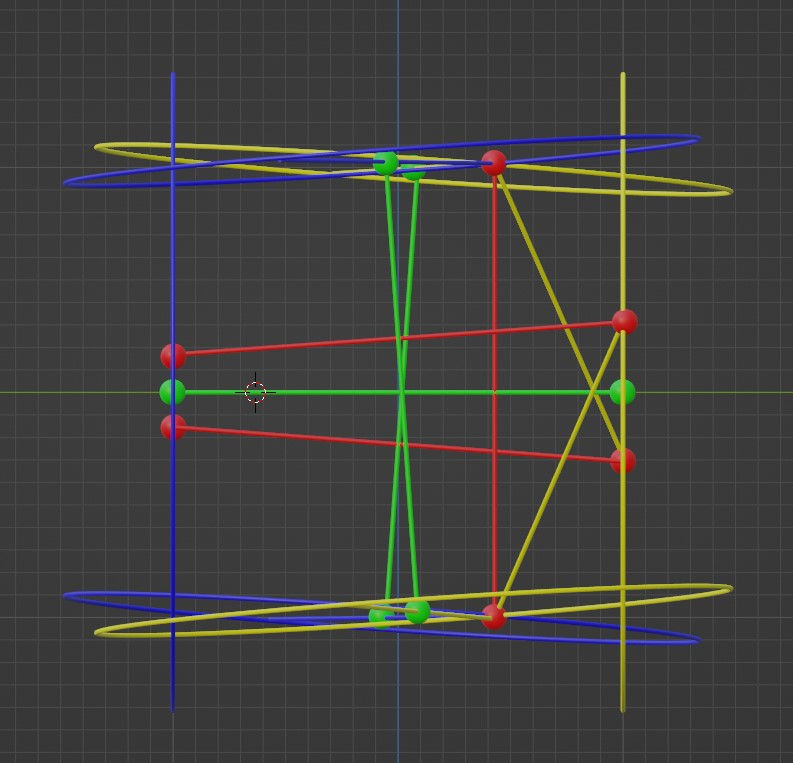
While I would so much like to say Q.E.D., I can’t. The above shape looks pretty good, but it still isn’t perfect. It might be that it only needs minor tweaks and it’s ready, but it’s also possible that masked behind the small imperfections, there’s some major error.
I would give myself roughly 50:50 odds that there are no major errors left and that I really am close to the final solution for the Theory of Everything. But because I’m also a realist, I’m still expecting at least one or two hurdles along the way.




Comments