I have been keeping a pause from my posts for some time because I’ve been dealing with the equations describing the vectors between neighboring dots in all matter. While I sort of knew what the equations would be, getting them to be precise has been laborious. While I’m pretty good at math, it’s still not my number one skill.
What I ended up finding to be the easiest approach to me was to sort of cheat. I knew I wanted the vectors to have a length of exactly one, because this simplifies the equations. Next, I wanted first to describe the case with no refraction. In this case the three first dots make an equilateral triangle with each edge having a length of one.
Then I semi-arbitrarily chose the three first dots to have the coordinates of
Where the column of three numbers represents the x, y and z coordinates. Each neighboring dots are connected with a vector:
Without going to the details why, I had figured out that the fourth dot must be
x in this notation is not a regular multiplication, but the cross product of two vectors, which is also a vector. Thus, the second term is a cross product of a cross product. The original vector:
and the two cross products define an almost cube (more accurately a right prism, because the length of the vectors that define the prism aren’t of equal length).
The fifth dot is defined by an almost identical equation, but where the sign of the second cross product is reversed:
And to be pedantic, we can universalize these into the equations:
And this is it! The perfectly simple equations of entangled dots with zero refraction. You can easily plot the dots in Excel, like this:
Apart from that there’s a very surprising problem: Excel’s inaccuracy. To some people this doesn’t come as a surprise. Even I had heard about this but hadn’t encountered this. You see, to make the mathematics easier, Excel cannot deal with an infinite number of decimal points. This means that when two slightly inaccurate numbers are multiplied, this inaccuracy is multiplied as well. At first this inaccuracy is almost imperceptible. You have to go to the sixteenth decimal point in dots four and five to see the difference:
The y coordinate is decreased by one, so the vector length is still one with an accuracy of thirty decimals (the maximum that Excel shows).
To begin with, this error is almost insignificant, but at a tipping point there is some sort of a chaotic effect, and the equations don’t work anymore, but rather produce vectors with a length of zero.
At first, I thought I would be working on introducing the orthogonal refraction, but this problem prevents me from understanding the long-term implications of the equations.
I can still see that introducing orthogonal refraction does seem to produce the expected helicity:
However, without resolving the accuracy problem of Excel, I’m faced with the chaotic nature of the equations.
But luckily I can pretty easily correct the error by always normalizing the length of the new vector by multiplying each component vector by the ratio of the length of the ‘ideal component vector’ to the actual length of the previous component vector. While this sound fancy, the equation is really simple, and you can make keep the array of vectors as long as you wish:
And this is what it looks like with orthogonal refraction:
This means that my mathematics is correct!
This also means that I proved (at least to an extent) that orthogonal refraction by itself doesn’t bend the helix, although it tilts it.
Next, I have to combine linear refraction with orthogonal refraction to see whether the combination of both is the solution to the need for bending.
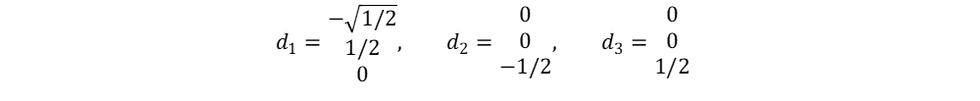
Comments