In today’s post I might have one of the two chiral unit spheres of reflection ready. The only problem is that if you include all of the rules governing reflection of elementary particles of energy (kaus/dots), you get a monster of a model. The projections look like this:
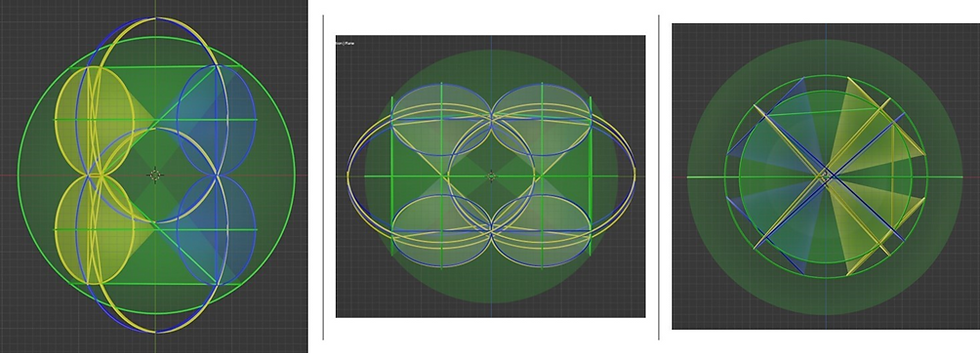
And the rotating 3D model looks like this:
I’m no longer sure whether I’ve included all of the rules used in this post in my previous posts. Possibly there are a few new things here that are to some extent new, even though I’ve talked about the principles around them before.
I know that the above model is a tiny bit off because it should include tilts both around the z axis (which it has) and a tiny tilt around the x axis (which it doesn’t have). Also, I can’t just copy this unit sphere of reflection and get the neighboring unit sphere. Making it’s chiral sibling requires me to reverse some of the tilts, which I won’t do until I get this shape converted into equations.
I must admit that the shape is making my head hurt a bit. There are just so many moving parts (mostly figuratively) that it’s too easy to make mistakes. So, that’s what I’ll be doing next. Adding the tilt around the x axis and finding the last flaws.
Also, looking at the above model, it seems that the tilts around the z axis cancel out in neighboring chiral unit spheres, but the tilts around the x axis sum up. This would explain the curvature of kaus reflecting after moving in tiny streaks in one-dimensional spacetime.
Comments