In today’s post I go back to basics. Or more specifically I find a structure that I had already presented much before, but this time just based on the knowledge that elementary particles of energy (dots) always move at the speed of light.
You see, I haven’t really based my Theory of Everything on strict mathematical principles before. I have more or less ‘cheated’ to get started. Rather than trying to prove my structures, I’ve thrown everything at the wall and tried to see what sticks. However, now that I have something that seems to stick, I can finally find proper mathematical proof to explain it.
So here we go.
First of all, the average distance of the dots from the center of the particle (for simplicity imagine we’re talking about a hydrogen atom) is a yet unknown large number (when the radius of a dot is normalized to one) R. But the dot’s will be at this distance only at two (or possibly a few more) fleeting instances during their orbital. Half of the time, they are further away from the center and half of the time closer. However, based on everything that I’ve found about the behavior of the dots, they always move at a constant angular velocity. From the illustration below we see that the non-reflecting component has to be longer the further away from the center the dot is. This means that the overall angle of reflection cannot be constant during their orbital.
The most observant reader might realize from the image that the average non-reflected velocity of the dots is c cos θ. This means that the average reflected velocity of dots is c sin θ. Without boring you with the details, it is quite easy to determine from the image what the maximum and minimum non-reflected and reflected velocities are.
To simplify a lot, this means that when you have four dots of a helix, as seen in the simplified image below, the dot above (A) moves slower than the one below (C), ultimately causing A to revolve around C in the opposite direction of their movement. If we consider B to move against A at a higher velocity, the parallel component of its speed with A is identical, but there also must be a rotational component that accounts for its larger speed. Also, in the same vein, the dot D, must consist of a parallel component of movement as B (and A), but its rotational component must be opposite, but of equal size, as that of B. It might not be obvious to you, dear reader, but this results in a secondary revolution, as shown in the below image, where the dot A is transferred from being the topmost dot to being the bottommost dot of the four.
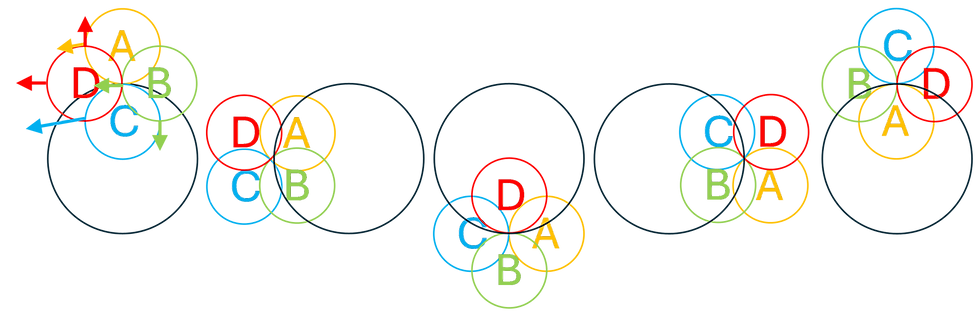
In real life this rotation takes place on the surface of a sphere. And for A to get back to where it started from, it needs to revolve twice. Also, while not exactly reflected in the above image, the distance in this projection between AB, BC and CD are kept constant after these reflections.
What I deliberately omitted from this second image is the gap between A and C, as well as between B and D, as shown in my previous post, as here the dots are from the same helix and not neighbors, like in “Making the Pi Bigger”.
Seeing all of this, you might ask “where are the dots reflecting from?” If the dots aren’t reflecting from the neighboring helix, as I proposed in my previous post, the only feasible answer is “they are reflected from the dots in front, as well as behind, in the same helix”. Only upon writing this, I realize that the reflection has to look like a continuously moving match of ping-pong. That is, dot B must take turns being reflected from A and C (and C being reflected from B and D). This is slightly similar to my original turn-by-turn reflection hypothesis, but with different dots being reflected.
If this hypothesis of “inter-helical reflection” holds, it should be pretty easy to turn into equations. However, I’ll have to leave that for future posts.
Comments