The Electron is a Spherical, Double-Helical Donut
- Kalle Lintinen
- Apr 7, 2023
- 6 min read
In my last post I realized that the basic structure of an electron must be a double helix, due to a rather complicated process and what I called ‘ugly maths’
Well, I went back to the Excel where I had doodled the double helix and realized that the math wasn’t that hard after all. I managed to simplify the equations to these:
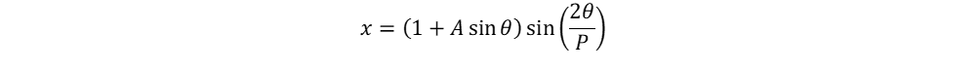
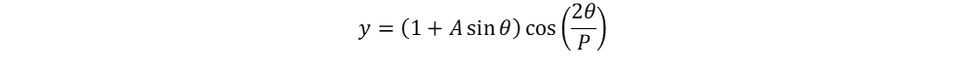
where A is the amplitude of the sine wave and P the number of periods in the closed loop. The image that I already showed had an amplitude (A) of 0.1 and the number of periods (P) of 15.
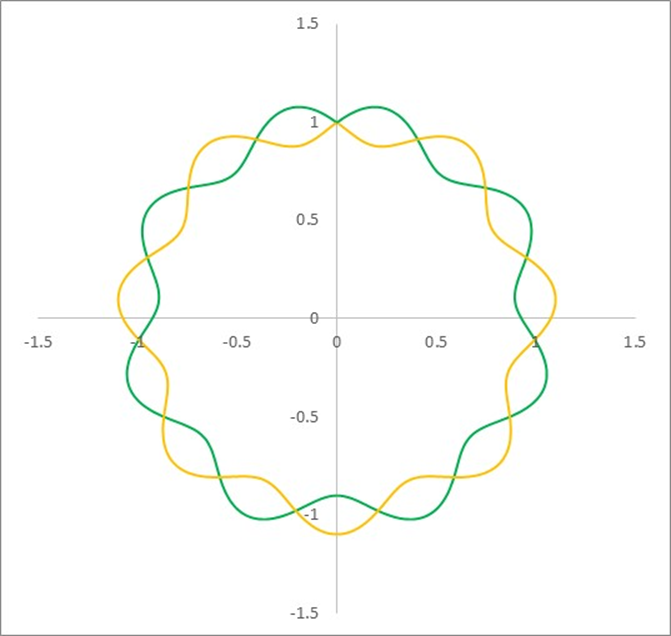
Then I started playing around with the equation and realized that the simplest double-helical closed loop is obtained with a P of 3.
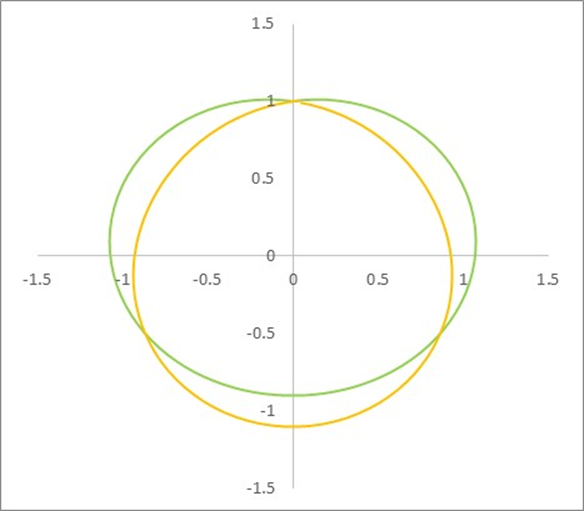
In the above image the amplitude of 0.1 is still way too high as a starting point. In reality the amplitude is probably close to the ratio of the Planck length to the wavelength of the gamma photon involved. However, in a scheme, this would just result in a circle.
So, what causes the amplitude not to remain infinitesimally small? It’s the observation that you cannot push a string. That is, the elementary particles, or dots, in the curve always move at the speed of light. But they are also confined by the dots surrounding them. This means that for the quasi-circular double-helical path to be maintained, the dots would need to push the dot ahead of it.
But as we know that the dots don’t push other dots, what takes place instead is that the dots ‘attempt’ to flow past the dot ahead. The only problem is that the 720 degree twist prevents the dots from moving freely. Exactly why this is, is more of an intuitive observation from my part. I can’t really easily explain why this is the case. You’ll have to trust me on this.
What this flowing past does is that it begins to increase the amplitude in the equation. When this happens, something odd appear to take place: the three helical twists begin to approach the origin, with the rest of the curve looking circular. In the below 2D plot the helical nature cannot be really seen, but soon I’ll show how it looks like in 3D.
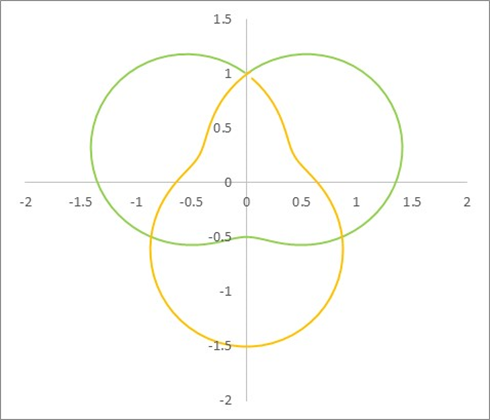
But this isn’t all. When the amplitude is increased to 1, something even more odd happens: the x-y projection of the 3D shape begins to look like a Venn diagram, but one where the area of the intersect is zero.
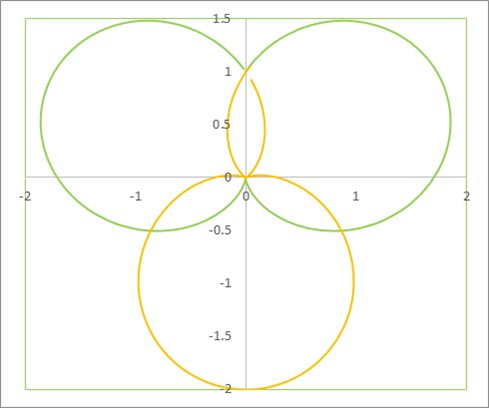
For a while I believed that this is a point of discontinuity. That beyond this point, something funky would take place. However, when I increased the amplitude above one, nothing ‘bad’ happened. The helical curve just passed the origin and a began to resemble petals in the 2D projection.
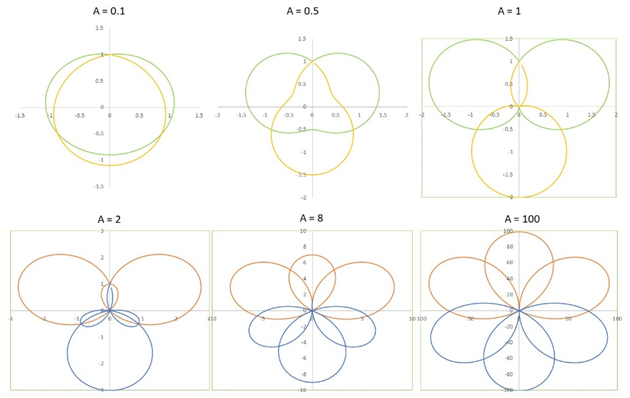
But looking in 3D, the shape looks quite a bit like my deuterium model, with a clear spherical symmetry. I have a hunch that this actually isn’t the way electrons form.

Rather, my intuition says that this is the shape of a boson, a carrier of force. Why would I think so? Because photons, which are also bosons, cannot account for all of the interactions between matter. But my knowledge of bosons is so wafer-thin, that I won’t say anything more than that. Otherwise I’ll just reveal the shallowness of my knowledge.
Next, I’ll revisit my statement from my last post:
There is a possibility that the amplitude of the wave is so big that in the end the electron no longer looks like a donut, but rather a ball. This would explain why the electron has always been considered not to have any particular shape. To figure out whether this is the case, I need a bit more time.
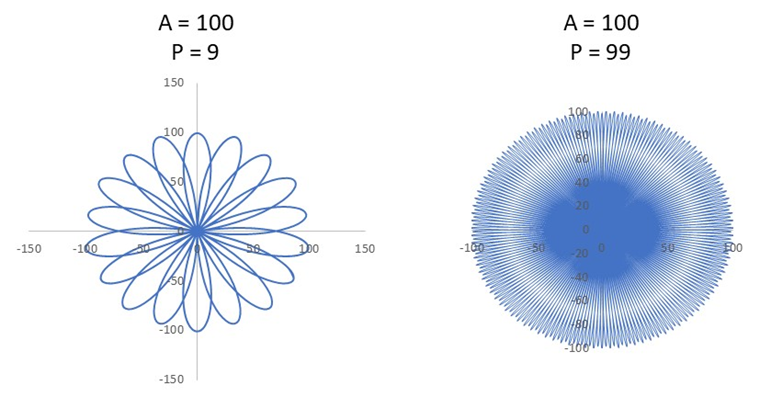
Almost not realizing it, I had illustrated the above principle for the spherical nature of the electron with the above ‘hexapetal’ geometry. The only problem is that it doesn’t appear likely that the number of periods (or turns) would magically increase without some external action. So, I decided to ignore for a while the attempt to explain how an electron would compactify and just tweak the constants of the equation and see what shape I would get. With an A of 100 and a P of 9, I could already observe 18 petals in the X-Y projection. And with an A of 100 and a P of 99, the shape was more or less spherical.
With blender, there weren’t too many problems when the shape was depicted with just curves, but with arrays of spheres, I started getting into challenges with computer memory. So I had to settle with a sphere count of 7670, which while being quite big for a human, is tiny with respect to the number of spheres required to accurately depict the shape.
However, something is better than nothing. Just imagine the shape below having an nearly endless number of arcs, where the spheres are infinitesimally small and packed close together, without any gaps.

Except, here we encounter a problem with this simple representation. The spheres (dots) don’t magically fuse together at the poles. Rather, the arcs must overlap at the poles in some rather neat manner, which allows for the spheres to freely move at the speed of light along the surface.
However, I don’t really know what this alignment is, as basic trigonometry doesn’t assume lines to have a thickness. While the above equations and illustrations are in my mind rather strong evidence for the electron to have a structure of a uniform spherical surface of a double-helical closed loop, my appetite for precision hasn’t yet been satisfied.
While the above shape looks pretty good, the problem with it is that the arcs fuse into each other at the poles. After some thinking, I realized that this is exactly the reason why you need the double-helical structure for the electron. Once you’ve made the helical cylinder with a distance of a single dot between the turns, the cylinder has to be dented from the side, so that when the cylinder is twisted for 720 degrees, there will be no fused dots. The dent has to be triangular, where the very central turns touch each other, but otherwise the touching turns are on opposite sides. Like this:
As I’m not at all good with creating these dents in blender, my first attempt is ugly, but conveys the idea.

Besides being ugly, the problem with using an array of spheres is that my computer doesn’t have enough memory to make these shapes. It just freezes when the number of spheres in the array is increased beyond roughly 10 000.
So, next I just ditched the array of spheres to save on memory and used a beveled curve instead. The curve itself is without thickness in Blender, but you can go to the geometry tab of the curve, add a round bevel with a suitable depth. Next, I learned how to do the deformation in a pretty way. I added a lattice (more specidfically a rectangular cuboid) around the curve before bending, when it still looked like a cylinder and then deformed the lattice to look like this:

This bent the cylindrical Archimedean helix just in the way, where the arcs wouldn’t fuse in the intersection, but would stack one on top of the other. And here is how it looks like, still with way too few arcs in comparison to an actual thick surface, but otherwise valid.

Ok, there is just one tiny thing to adjust. The deformation of the lattice cannot be 100 % symmetrical, as this causes the neighboring arcs still to fuse, even though the rest of the structure looks ok. But this should be corrected relatively easily. I could do this manually with a sphere made with a helix with just five turns.

Next, I have to decide whether this is good enough to publish. I think it is, with the caveat that next I actually have to write everything down, using proper scientific language. This will still take some time and I’ll probably figure new things out in the process. I think I at least need to include the deformation of the cylinder into the equations.
Now I finally have a good feeling about the likelihood of convincing the reviewers. It doesn't seem there's any magical or miraculous thinking left in this model.




Comments