I've been rather quiet in the last few days, as my posts on solar fusion turned out to be much more fruitful than I had originally considered.
If you've read those, you might remember that my idea of the first step of the proton-proton chain involves the flipping of hydrogen orbital into its mirror image: a neutron orbital. I think I already noted that the this flipped orbital isn't actually the fused orbital of the deuterium, but rather in the high pressure and temperature of the solar core, the orbitals undergo string transfer (I used the term chain transfer a metathesis, but I think the only correct term must be string transfer, as this is literally what takes place).
So in previous posts I presented you with the below image, but knew that this strained state is only an intermediate that relaxed into an orbital that fits eight loops into a space that used to fit just four.
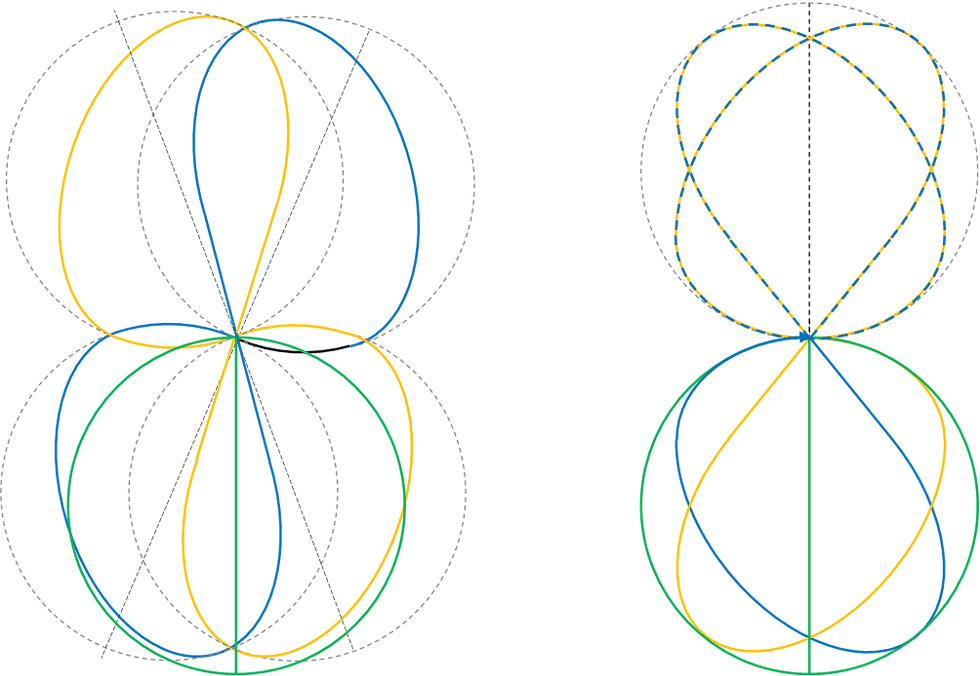
So, for the last week, I've been figuring out the trigonometry of the orbital, considering that it consists of Planck spheres moving at the speed of light. So any collisions between Planck spheres in orbit must be symmetrical and allow the conservation of momentum.
After several unsuccessful attempts I ended up with the below (x-y) projection that looks like the petals of a flower.
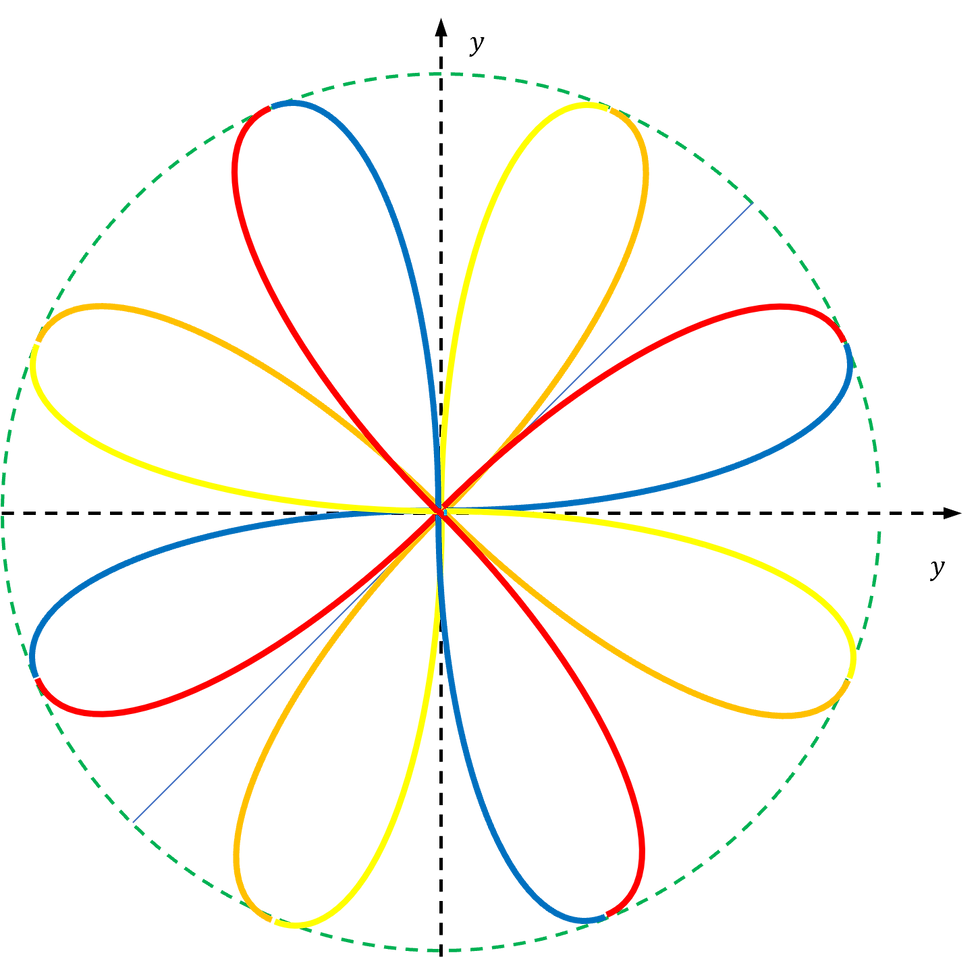
It must be rather impossible to understand its three-dimensionality, so here is a (still rough) 3D Blender rendering of the orbital. From the 3D model one observes four loops, where the neighboring loops is always mirror images of each other. Due to this chirality, the loop is at a 45° angle at the top (blue and yellow arcs) compared to the bottom (orange and red arcs) .
For clarity, a single loop is drawn with two colors. Either blue/red or yellow/orange, depending on the chirality.
The astute observer notes at this point that I am presenting an orbital around just one sphere, while I've shown previous orbitals around two spheres. This is because I am not yet 100% sure whether deuterium fusion takes place on both sides of the orbital or not.
Next, I need to calculate the combined lenghts of these arcs and compare them to the lenghts of the arcs in the hydrogen orbital. If the difference in the lengths corresponds with the binding energy of deuterium, This model has a decent chance of being reflective of reality and not just rather pretty 3D flower.
Comments