In today’s post on my quest for the Theory of Everything, I realize that there is a rather simple equation to define the distance of two neighboring elementary particles of energy (dots) at the point of their reflection.
In my previous posts I’ve talked about the reflection of two dots from one circular plane to another. And in other posts, especially in the last one, I’ve talked about two dots grazing each other at a distance of twice the radius of a dot (2r). I’m not sure whether I’ve mentioned it, there must be two angles of reflection for the dots. Possibly I’ve used other symbols for these, but in this post, I name the smaller angle of reflection α, or alpha, and the larger angle of reflection β, or beta. The angle α is the one closer to the point where the two circular planes of reflection meet and β is the one farther away. One can see why α is closer by looking at the figure below.
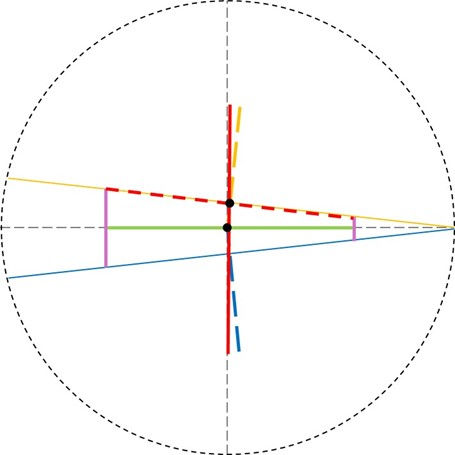
The rather short purple lines are the sine components of the distance of √8r that each dot travels between reflection. Thus, the length of the shorter purple line is √8r sin α, and conversely the length of the shorter purple line is √8r sin β. Similarly, the length of the components of the purple lines perpendicular to the plane defined by this screen are √8r cos α and √8r cos β. This means that at the point of reflection the dots are separated by a distance of 2r in the horizontal direction, √2r (sin β - sin α) in the vertical direction and √2r (cos α - cos β) in the direction perpendicular to the plane. Thus, using Pythagorean theorem in three dimensions, the distance between the dots is:
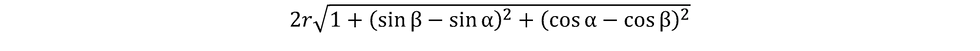
This means that one can take this distance, marked in red dashed lines and define the distance between the two particles being reflected, marked with a solid red vertical line. However, it is of note that in the above image the length of the solid red line should be longer than the dashed red line, because it only shows a length of
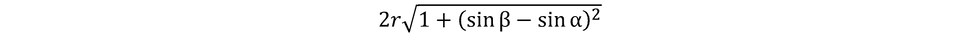
I haven’t figured out the mathematics much further than this. However, I think you can stack the figures one on top of each other. Something like this:
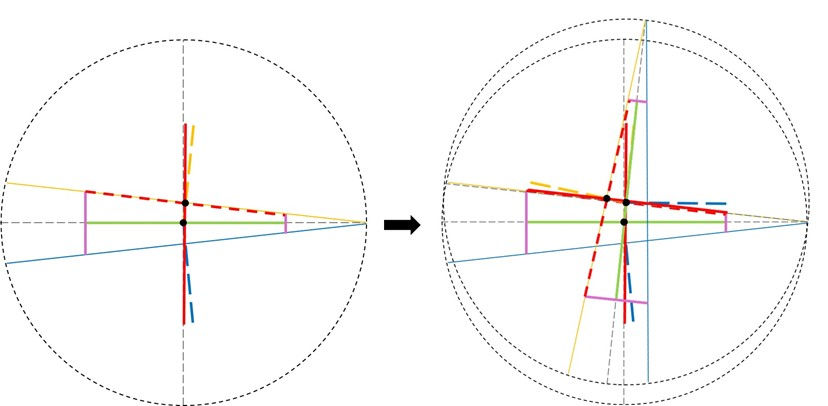
I’ve added black circles to indicate the center points of the four dots moving in orbit at each point of reflection.
I was thinking that I would have more to say about this, but I think this is it for today. Let’s leave this on a cliffhanger…
Comments