The Cross and the Graze
- Kalle Lintinen
- Nov 16, 2024
- 2 min read
In today’s post on my quest to explain the Theory of Everything through the reflection of elementary particles of energy (kaus/dots), I edge one step closer to the 100 % precise geometry of reflection. And to aid in this I need both Cross and Graze. And despite the possible biblical connotations to some readers, I’m still referring to geometry.
Just to make things a bit more interesting, this is what the Cross and Graze looks like in 3D:
And now I’ll explain what I’ve shown to you. The crosses in the above model present the connections of both the grazing vectors, as well as the distance between reflecting dots that don’t really touch, or even graze. While the length of the green grazing connection vector is exactly 2r (double the radius of a kau/dot), the length of the green reflection connection vector is a bit larger than 2r, but I won’t explain why in this post (I’ve explained this in previous posts). These two vectors don’t describe the same point in time in the path of the kaus/dots, but there’s no reason why we still couldn’t show them together.
When you add these crosses to the reflection projections, you see how the addition of the cross connects the otherwise ‘loose’ elements:
Here’s the y-z projection:
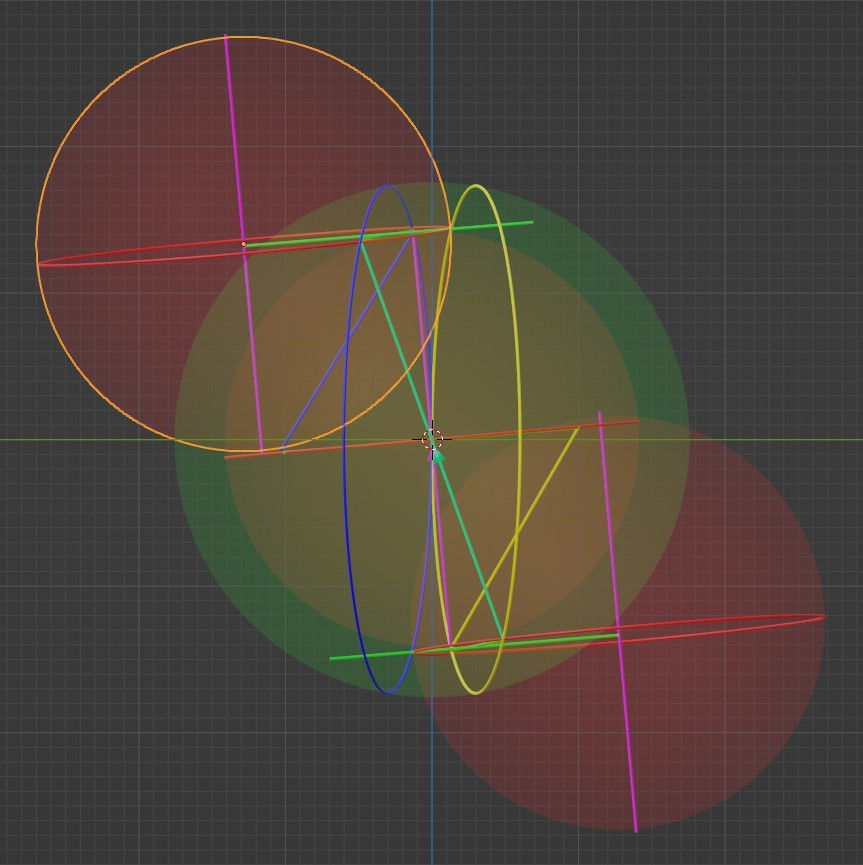
Here’s the x-z projection:

And here’s the x-y projection:
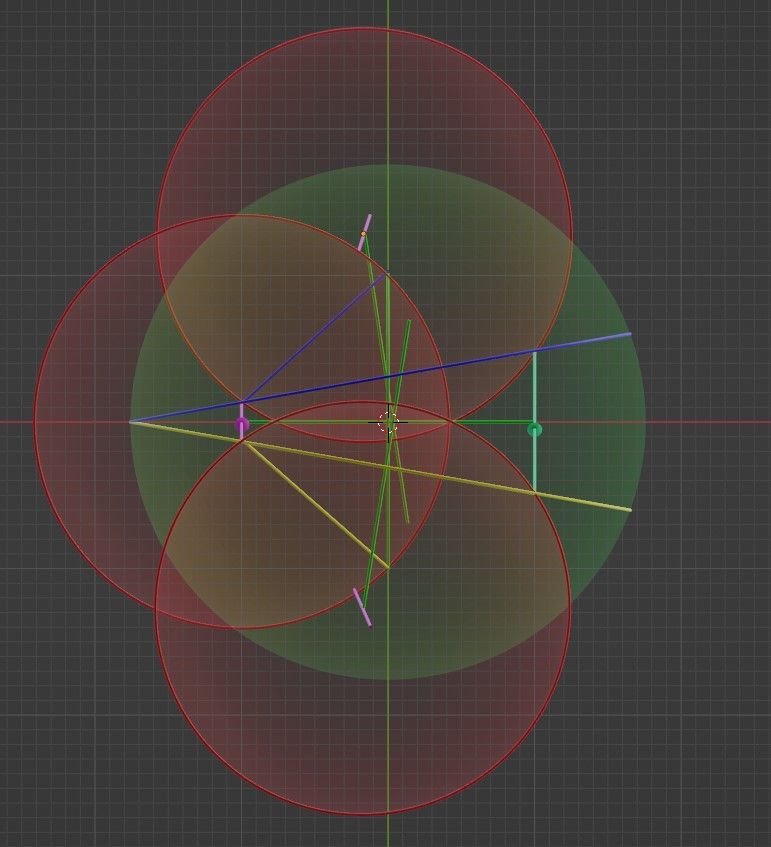
If you look closely, I’ve made tiny corrections to the geometry from the Kau particle post, but the shape is still a little bit off. I think the reason is that the geometry requires the flight path between reflections to be much longer when the angles are as exaggerated as in this model. But there might be some other reason as well.
Although, what you see here isn’t the final answer, I’m convinced that the final answer lies in the Cross and the Graze.



Comments