Precision Reflections
- Kalle Lintinen
- Sep 24, 2024
- 4 min read
In my last post on the quest for the Theory of Everything, based on the reflections of elementary particles of energy (dots), I had already created the mathematical tool that I call the tetracone of reflection, which I applied to my model of reflection from one circular plane to another. As the tetracone of reflection is highly intuitive, I could place a pretty good mockup of the shape onto the rest of the model rather easily. However, a bit more effort would go to aligning the vectors of reflection onto the shape.
So, this post is about placing the precise vectors of reflection. But first, before going into explaining the results, I’ll take you to how I got there. You see, the tetracone of reflection itself isn’t some magical solution in itself, but a tool that helps me draw projections and design 3D images based on these. To be frank, once the tetracone showed the idea for the geometrical solution for reflection, the rest was pure geometry.
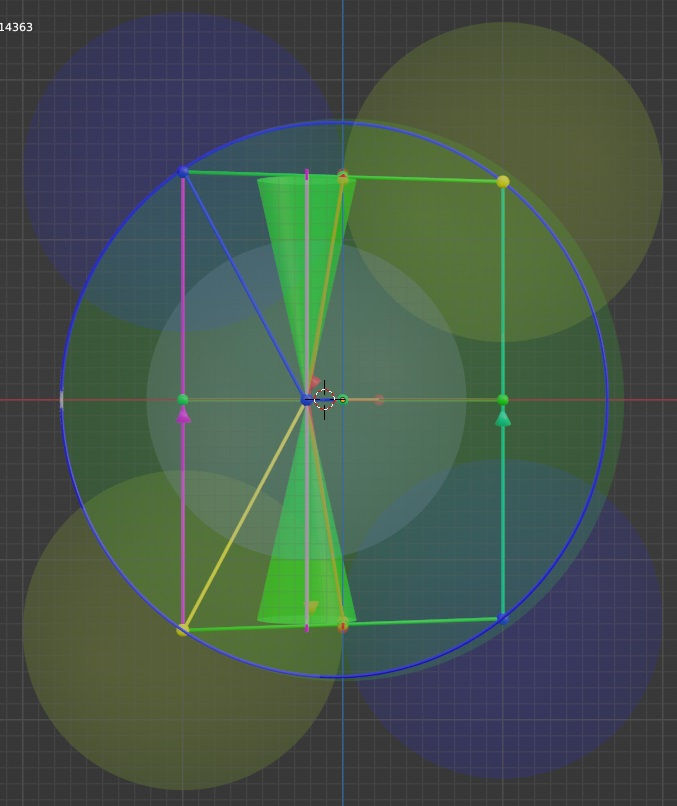
Below you see the reflection tetracone in the x-z projection. And the reason you see only one tetracone (with the cones at the tips omitted) is that in this projection the two reflection tetracones perfectly overlap. The approaching and reflecting vectors are drawn in red and are barely visible behind the tetracone. The linear vector from which the red vector is reflected from is colored purple. The actual movement is from the yellow to blue dot on the left, but the same vectors is also drawn through the central blue and yellow dots, so that it passes through its center. The point where the central dots are moving towards is marked by a red dot at the end of the red reflection vector. This dot must be located at exactly the middle of the vector drawn from the top blue dot to the top yellow dot. While this might not be obvious, these two dots do not touch each other. This means that while the location of the central blue and yellow dots are shifted left along the x-axis to begin with, they will move to a point where its location along the x-axis is zero.
Next, let’s look at the y-z projection. There you can see the two reflection tetracones on ether side of the center at the same angle (obviously) as the purple vector depicting the movement of the dots closer to the connection point of the two circular planes of reflection. The vectors of approaching and reflection of both the left blue dot and the right yellow dot are shown both in their actual place, but also shown shifted in the center. When viewed this way, it is clear that the approach and reflections from the left are seen on the right side of the vertical z axis when sifted towards the center and the vectors from the right are shifted to the left.
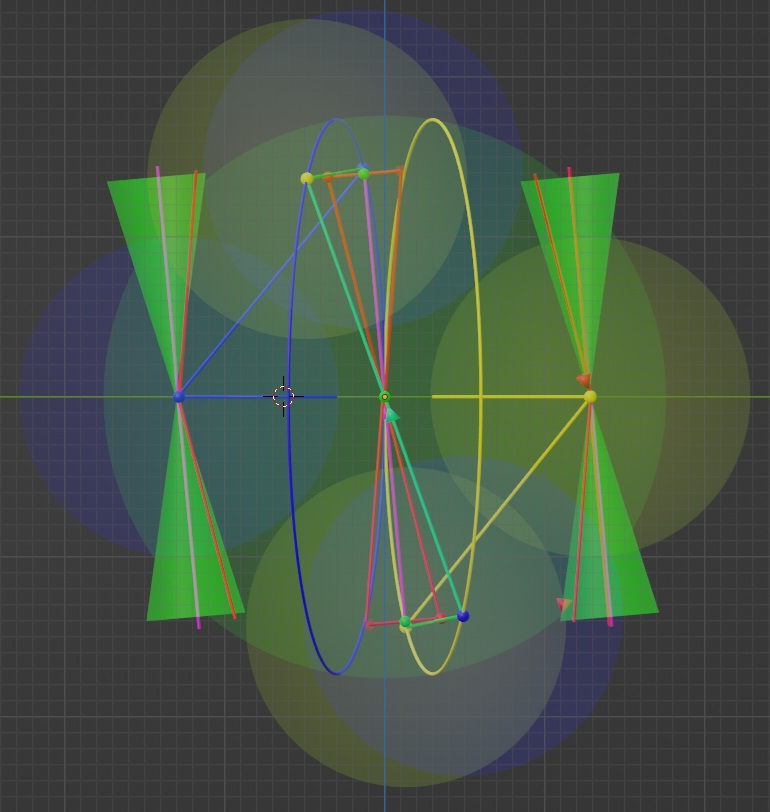
If you look at the picture very closely, the whole concept of this sort of reflection feels very unintuitive. Looking at the yellow dot on the right, the dot is being reflected towards the yellow bottom dot with which the right yellow dot is being reflected with. How can this be? Well, the yellow bottom dot is also being reflected by the yellow right dot, making it move further away from the right dot. That is, all of the four dots in the above image (and rest of the projections) are moving away from each other.
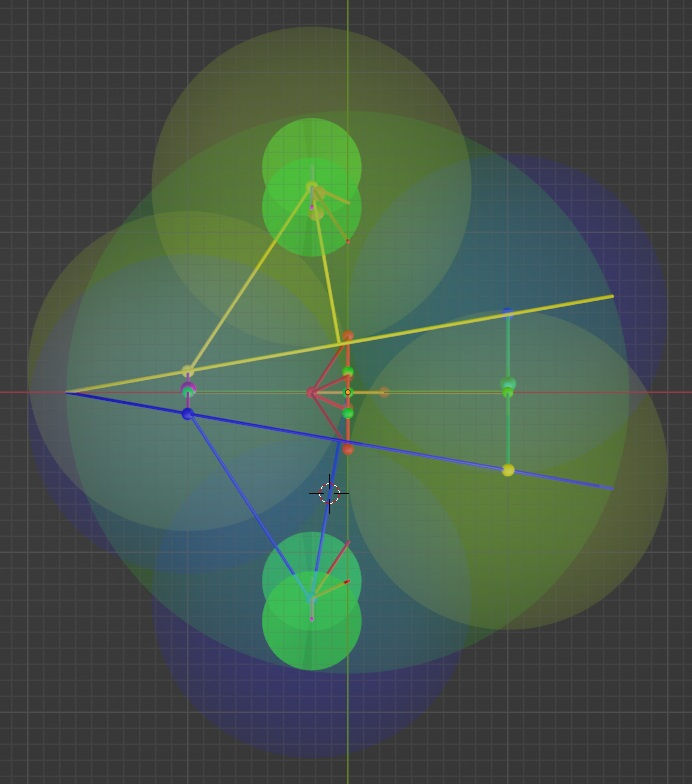
Next, let’s look at the x-y projection. At the center you see two reflected paths shaped like sharp Cs, one above and one below the horizontal line. These Cs are the same approach and reflection vectors you saw in the y-z projection.
And this is what the model looks like rotating:
As the title of this post says, this is already looking much more precise than ever before. However, I notice that I feel tempted to read much more into the above model than the model allows. It’s like seeing Jesus in a toast, or Pareidolia, to use a fancier phrase. Even if I could find some other patterns from the above shape, they won’t mean anything, unless they can be linked to the reflection of dots. These patterns can be an intuitive hint to dig deeper, but unless there is something more tangible behind the pattern, it’s best to keep silent.
But getting this far isn’t too bad for single day’s work. I’m quite sure it won’t take too long for me to be able to accurately combine two of these models to understand how reflections are ‘stacked up’. And once I get two models to stack up, I can make however many models to stack up as I like. And if everything is precise, stacking enough of these models up, I should get a closed-loop orbital of dots. And this should be the proof that the reflection of energy can explain the existence of matter.




Comments