On Helium and Fusion
- Kalle Lintinen
- Sep 16, 2022
- 7 min read
In the past posts I have talked about hydrogen and have been able to describe at least some of its concrete properties based on the model of discrete supramolecular shell, with strings of Planck spheres moving at the speed of light. I’ve also been quite open about being unsure what atoms more complex than hydrogen look like on the level of strings.
Today I try to wrap my name around the elusive molecule first found from the sun, before being found on Earth. Hence its name helium, derived from the Greek work for the sun, helios. Unlike hydrogen, with only a single proton at its core, helium has two protons and two neutrons. While the two protons are involved in chemical bonds, the two neutrons binds the protons into a stable nucleus, but are not involved in in chemical bonds. Or more specifically, there could not be a helium isotope with no neutrons. Even the isotope with just one neutron can only be found deep in the earth's mantle where it was trapped during formation of the earth.
Just like with hydrogen, we have never observed a single helium atom. This is not to say that such atoms do not exist, but that we have no means to image a single helium atom unbound to other atoms. What this means is that the assumption that the helium atoms move randomly, unbound to other helium atoms, has not been proven: just postulated.
Rather, there actually are helium compounds, such as disodium helide, which is only stable under immense pressure. The Wikipedia page states “The helium atoms do not participate in any bonding. However the electron pairs can be considered as an eight-centre two-electron bond.” With some Wikipedia knowledge, this means that it is an electron-deficient chemical bond where eight atoms share two electrons. So, as far as I understand, what is stated that there isn’t a bond, but there actually is, if you extend the definition.
And if you go far down in the Wikipedia page of Helium, the whole concept of Helium not forming bonds becomes rather dubious. Rather, it appears that the bonds between helium atoms in the supramolecular shell are so stable that the supramolecular shell won’t easily break and incorporate other atoms into it.
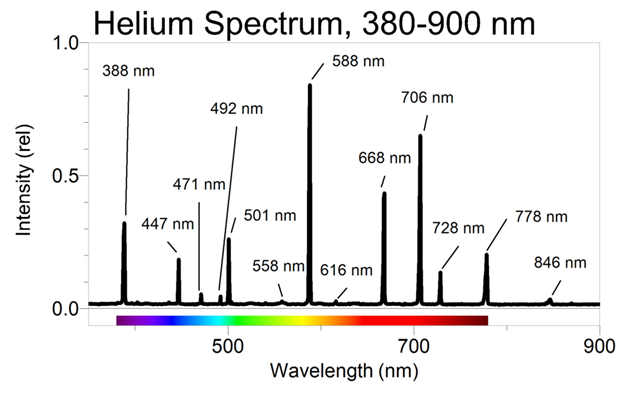
So how large is the supramolecular shell of helium? The first clues about its size are in its spectral lines. The main peak of 588 nm is the same Balmer n = 3, n'= 2 as I used in the example with hydrogen. This appears to indicate that the most common size for the supramolecular shell is 588 nm/3 = 196 nm. This is only slightly smaller than the 656.3 nm/3 = 218.8 nm for hydrogen. At least superficially it appears that hydrogen and helium are not too different after all.
Next, we need to think about how the four almost identically sized orbitals are arranged in helium. Traditional pictures describe protons and neutrons as a cluster of spheres, but this image doesn’t seem to make much sense based on most of the mass of the protons and neutrons being in the orbital and not at the core. If we consider quarks to be true particles/rings, and not just phenomena of atom-smashing, the protons/neutrons could be clusters of these quark rings.
If not for the neutrons, my guess for the structure of helium would just be a structure, where the two orbitals of the protons interlock at the center, but where the orbitals would form an X. This way, the helium atom can bond in four directions of the supramolecular shell, with two bonds within the same loop and two bonds with neighboring loops.
This model isn’t impossible even when there are one or two neutrons involved. However, first we need to consider what neutrons are. The difference between a proton and a neutron can be found in the sentence “A free neutron spontaneously decays to a proton, an electron, and an antineutrino”. For scale, the mass of a proton, electron and antineutrino are 938.27 MeV/c², 0.511 MeV/c² and < 0.120 eV/c² (note: over six orders of magnitude smaller than the electron). So, with an accuracy of 99.99999999 %, the mass of the neutron is the mass of proton plus the mass of the electron. Based on my previous blog post, the electron is just the cleavable portion of the orbital and not truly separate entity. Thus, it can be safely said that the proton/electron orbital and the neutron orbital should be otherwise identical, but that only the proton/electron orbital partakes in reactions. That is, apart from nuclear reactions that are much less common.
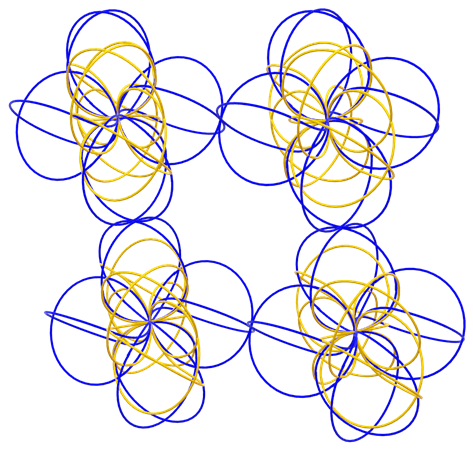
My educated guess is that the neutron is just the proton/electron orbital flipped 180° around itself, so that the proton/electron orbital and the neutron form a ‘butterfly pattern’. This is shown in the scheme below, with the blue orbitals indicating proton/electron and the yellow orbitals indicating neutron. The scheme gives my best guess of the whole helium atom, with two proton/electron orbitals and two neutrons. I couldn’t tell whether the angles are perfectly correct, but it looks just about right.

Next, we can look at how the helium atoms form bonds with neighboring proton/electron orbitals, forming a ‘fishnet plane’
However, in this case the orbitals of neutrons are pointing up and down and not only along the ‘fishnet plane’. While it may sound counterintuitive that neutrons would be unreactive, despite being almost the same as the proton/electron orbital, this appears to be the nature of ‘chirality’ of the orbitals. In chemistry, chirality is the mirror symmetry of molecules. However, there is a concept of chirality in nuclear physics as well, although I am not at all familiar with it. Or more specifically, the neutron is a mirror orbital of proton/electron. This appears to indicate that neutrons are chemically inactive. However, whether they have a role in the cleavage of electrons from the proton/electron orbital is yet unclear.
Next, we have to address the elephant in the room. That is, the nature of nuclear reactions. That is, why is the mass of helium 4 isotope smaller than the sum of two protons, two electrons and two neutrons? Conventionally we talk about the binding energies. Or more specifically “Nuclear binding energy in experimental physics is the minimum energy that is required to disassemble the nucleus of an atom into its constituent protons and neutrons, known collectively as nucleons.“
If we continue with the literal interpretation, where energy is a piece of string, this means that when the proton/electron and neutron orbitals fuse together in nuclear reactions to form a heavier atom, what is released is some of the string that makes up these orbitals. Thus, the only way to release these orbitals from each other is to add more string to the heavier atom, to separate the orbitals from each other.

For a light lesson in nuclear physics, we know that when hydrogen is fused into heavier elements, energy/string is released more or less up until the mass of iron has been reached. The image below shows that the steps are not linear. For instance, helium has a much larger binding energy than lithium, despite being a lighter element. However, as a general rule, the binding energy increases up to iron, where it peaks. After iron, the binding energy decreases again.
All commercial nuclear power plants take advantage of the fission reaction, where (almost exclusively) uranium is split into lighter elements. This is rather ‘easy’ to achieve, compared to the other nuclear reaction, that is fusion. To some extent, nuclear fusion is the most common reaction in the universe, as this is what occurs in all stars. However, the very gradual process of fusing hydrogen plasma into helium that takes place in stars is not something we would wish to emulate on Earth. While the process is ‘efficient and reliable’, it is isn’t very energy dense. That is, to obtain the conditions at the core of stars, we would need to put more energy to maintain the system than we could ever get out. This is why any attempts at fusion energy on earth look very different from what goes on in stars.
The most far advanced technology (or at least the one with most money sunk in) is TOKAMAK. According to Wikipedia “a tokamak is a device which uses a powerful magnetic field to confine plasma in the shape of a torus. The tokamak is one of several types of magnetic confinement devices being developed to produce controlled thermonuclear fusion power. As of 2016, it was the leading candidate for a practical fusion reactor.”
So what takes place in the fusion reaction? At least in a TOKAMAK, you take two isotopes of hydrogen: one deuterium (one proton/electron and one neutron) and fuse it with one tritium (one proton/electron and two neutrons). You end up with helium (two proton/electrons and two neutrons) and a free neutron, which reacts with deuterium to form more tritium.
As far as I understand it, the biggest problem is how to confine the reactions with magnets to be just 1° deuterium + tritium -> helium + neutron and 2° deuterium + neutron -> tritium. If everything isn’t perfect, the molecules/neutron react with the walls of the TOKAMAK and the fusion reaction fizzles out. As of yet, the record power in/power out ratio is 24 MW/ 16 MW, with Joint European Torus, or JET (already in in 1997).
While nothing to be sneezed at, the above ratio means it hasn’t broken even. This means that JET can never be used to generate power. However, this is one of the main objectives of ITER, the next generation fusion reactor. Or to be more precise, ITER attempt to generate more power than it consumes. However, it will never produce electricity because electricity generation is experimentally uninteresting. That is, it if is shown that electricity can be generated with fusion power (specifically with the ITER setup), the next step would be to design a commercial power plant based on the ITER design. Not to use the experimental reactor itself.
As a chemist, my views on fusion power are reservedly optimistic. If it can be harnessed on Earth, it would be great. However, if we find that there are engineering challenges in the process that are unsolvable, then we must accept defeat. But to my understanding the problem is that to figure out whether we can solve the engineering challenges requires funding on the scale of the Manhattan project. Most importantly, we haven’t proven that terrestrial production of electricity with fusion power cannot be done.
If I could help even in some small way with this supramolecular approach in understanding the conversion of hydrogen into helium, I would be a very happy man.




Comments