In today’s post on my quest to explain the Theory of Everything with the reflections of elementary particles of energy (dots), I introduce a sneak preview on the shape of the complete unit cell of reflection. In my last post I presented the basic concept of this unit cell, but because I wasn’t yet able to introduce accurate grazing rings to the shape, which made the whole first attempt extremely wonky.
This time I think I have sorted the wonkiness problem. Once again, the solution is with spacetime tetragons. You see, the original spacetime tetragon that I introduced two months ago described a shape which was otherwise identical to the grazing rings. The curious thing is that once I added the spacetime tetragon to my initial unit cell, it seemed that there was absolutely no reason whatsoever why I didn’t know how to add the shape to begin with. Here is what the rotating model looks like:
With the model rotating, it might be tricky to see all the individual parts of the model. Let’s look at the y-z projection first, as it’s probably the easiest to explain. The grazing vectors are obviously the two ellipses with vectors drawn through them. The axle of the grazing ring is a nearly horizontal tilted cylinder.
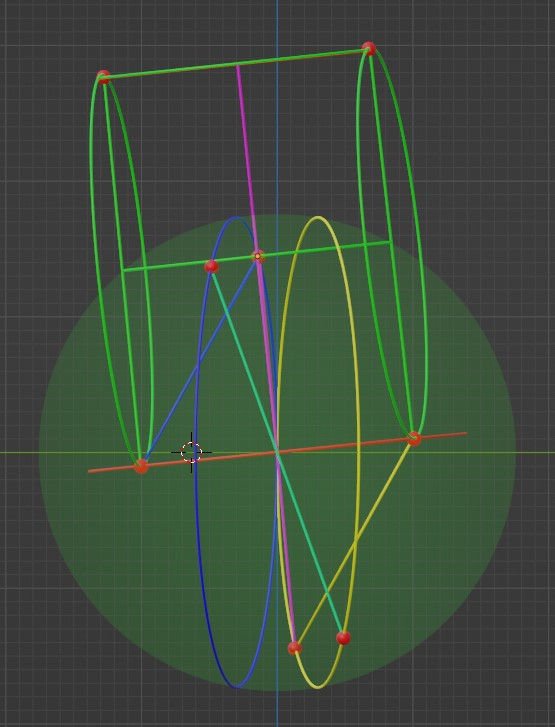
Next, let’s look at the x-y projection. There you can see that the axle of the grazing rings isn’t just tilted around the x-axis, but also tilted around the z-axis as well. While it can’t be seen in the y-z projection, here it is obvious that the grazing vectors point to opposite directions along the x-axis.
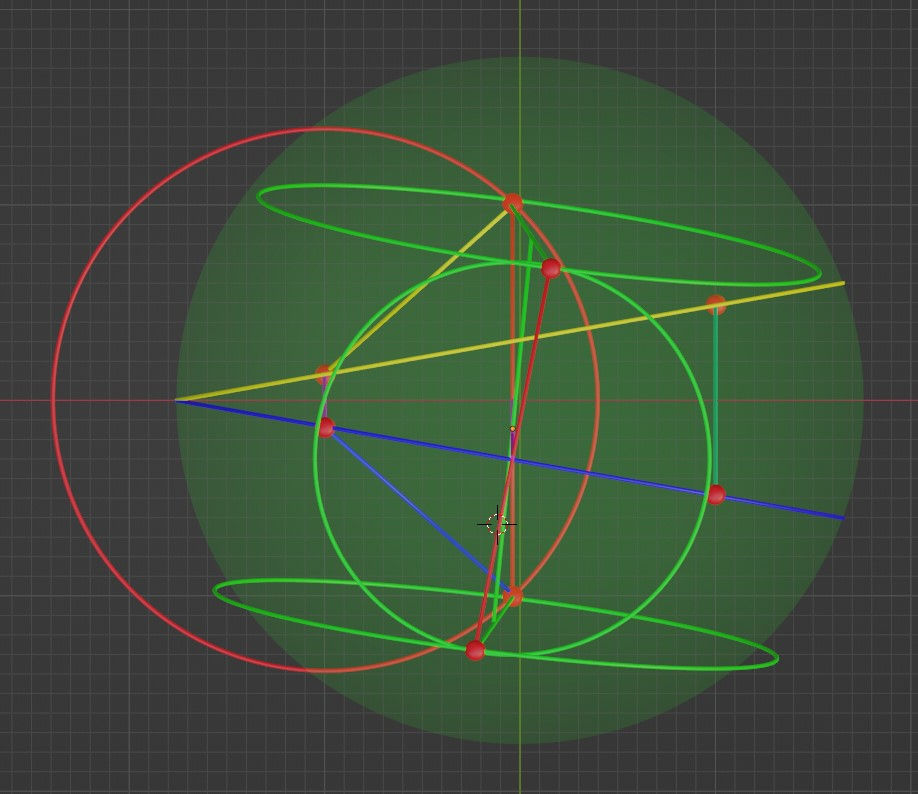
And here you can see the x-z projection, which to my mind shows the identical nature of the grazing vectors and their connections with the spacetime tetragon.
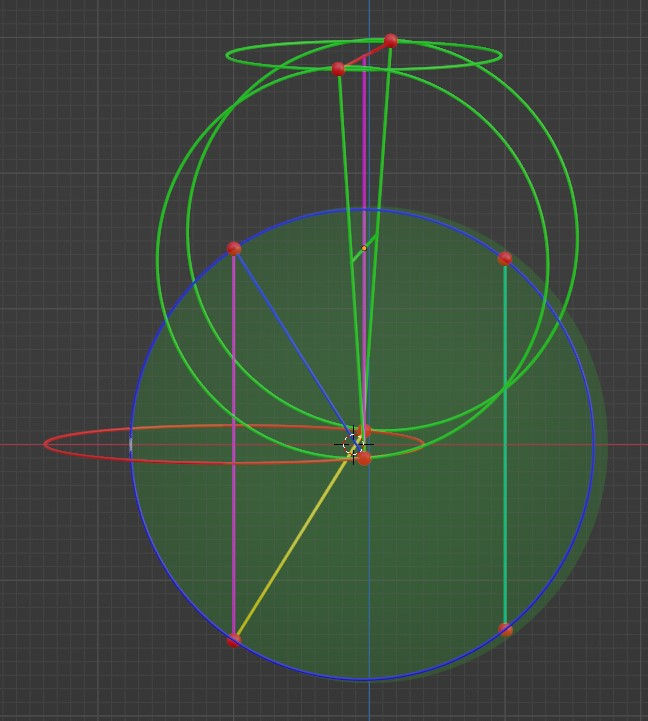
While I haven’t shown the grazing rings for the central shape, I could very well add them. When they are added, this is the first accurate stacking of two neighboring grazing wheels. Or at least it ought to be. The above is a visual proof of the concept. I still need to convert the above shape into equations to be absolutely certain. I’ve been quite confident before, only to have been corrected by the equations not making sense.
However, I’m quite confident that if I find errors in this logic, they will be only minor ones. Famous last words…
Comments