Already a month ago I posted about the The Mathematical Bits and Bobs of Everything, or what the supplementary information of the Theory of Everything holds. Today I introduce better bits and bobs. Or more specifically the revised supplementary information.
In the previous post I told you that the only new thing that I could explain with a simple image was the coupling of the rotations of supramolecular shells.
This time I attempt to explain the folding and knotting of an orbital. You see, the fancy equations that I show in the manuscript look pretty much undecipherable, but if we reduce the equation to the simplest possible form, the equation becomes at least a bit more understandable.
Below we have Figure S2 of the new supplementary information. It shows the shape of a loop folded over a spherical volume (an imaginary ball, so to say). The size of this imaginary ball is chosen so that if you pull the loop tight on either side of the ball, the loop touches itself at either side. Looking from above (a), the shape looks like four petals of a flower, but from the sides it looks like a teardrop; either a right-way-up one (b), or an upside-down one (c).
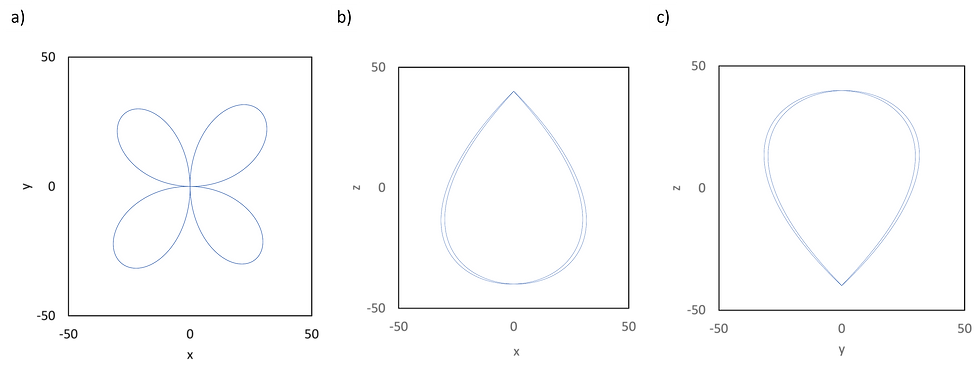
Figure S2
So how does this petal/tear drop stay folded? Well, the magical answer is, that it doesn't. Not unless the loop is knotted at either end. And does it? As far as I know, not with four loops.
The problem with the above shape isn't just that it needs to knot at two ends, but is also has to curve much more than if the four loops could encircle two imaginary balls instead of two. The equations depicting Figure S2 were so simple that I could make the shape with just one equation for each axis. However, the equations for arrcs over two imaginary balls were at the same time individually simpler, as they were just circular arcs, but then again much more complicated, as I needed to fit these arcs over the imaginary ball.
Figure S3
With just a bit of handwaving I can explain why I need the orbitals to form a double-sphere. If I knew how to write a bit better, I wouldn't need any handwaving.
So, is the supplementary information ready? The hones answer is: "kind of, but probably not". Next I need to read it through with thought and then read the main manuscript and think long and hard whether there are any major holes. I'll have to be content that there will bound to be minor holes that I won't see now, but which will be self-evident once they are spotted out to me.
It sure seems I'm awfully close to being able to submit the manuscript. I thought I would get someone else to read the manuscript with though and give comments, but it seems the effort of finding such a persons is better spent just working on the manuscript by myself.
Comments