While in my last post I attempted to the best of my abilities to present the theory of everything in a language that's understandable to non-scientist, today I'll talk about the mathematical bits and bobs that are required to understand the finer details of the theory, but which are too heavy to include into the main manuscript.
These bits and bobs are called the supplementary information or supporting information (depending on the publisher). Oftertimes important publications in Science and Nature require published articles to be compact and polished. This means that all of the other information that backs up the claims that are made in the published article, will be published as well. If the article isn't that important, the supplementary information can be forgotten and not viewed by many. However, for some articles, the supplementary information becomes just as important, and sometimes even more important than the published article (or the main text).
In my case I've struggled with what to include in the main text and what to put into the supplementary information and what to leave out of peer review altogether. I've mentioned before that if you include decent evidence to back really good evidence, the decent evidence doesn't improve the argument in the reader's (or listener's) mind, but rather causes the reader/listener to consider the really good evidence to be only decent. This is why it is suggested to only show the best available data to be as convincing as possible.
So I'm trying to heed this advice, but still include the most important evidence of my original manuscript, which I now consider a bit outdated, but partially valid. I only started rewriting the supplementary information just now, so it might still hold some errors. However, now that I have the main text pretty much ready, I'm able to make the supplementary information much more logical than before.
Unfortunately for you, dear reader, this text is not layman friendly. Probably closest to something understandable without too much background knowledge is the theory of the coupling of the rotations of supramolecular shells shown in the image below.
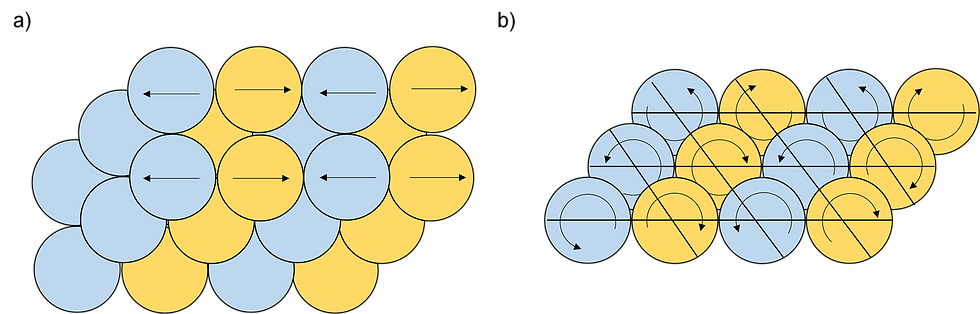
Let's see whether I can explain this simply enough. The blue and yellow balls you see above are supramolecular shell either rotating clockwise (yellow balls) or counterclockwise (blue balls). In a) you see them from above. Like gears in a machine they can freely rotate, just as long as the direction of rotation of neighboring spheres is opposite, unless the axis of rotation of neighboring balls is the same, in which case their direction of rotation should be the same. In b) you see the same thing as in a) but from the side. While it looks like that the spheres of the same colour on two layers touch, its possible to have them not touch, if you lift the layers up just a little bit, so that nonen of the spheres of the different layers no longer touch. If you then shift the layer tiny bit to the right, then the spheres of different colour
different colour still touch, but the spheres of the same colour no longer do. This way you can have a sea of rotating spheres where the spheres in direct contact are always rotating in opposite directions. This is actually pretty easy to verify experimentally.
Anyhow, here is the current supplementary information for those of you brave enough to read it.
Comments