Baby Steps Towards Perfection
- Kalle Lintinen
- Nov 2, 2024
- 2 min read
In my last post I talked about the difference between crackpot science and true science. Or even more specifically the difference between crackpot mathematics and true mathematics. In proper mathematics, you cannot have a step of “Then a miracle occurs”. If you’re a reader of my blog, you know this refers to my quest to explain the Theory of Everything with the reflection of elementary particles of energy (dots). In the post, I also presented my latest reflection model, which I promised was “non-crackpot” in nature.
However, even when presenting the shape, I knew I had taken a couple of shortcuts. The shape looked good, but it wasn’t perfect.
As the title says, in today’s post I take baby step towards Perfection. And again, I’m not at the stage where I could be presenting equations, because I’m still dealing with trigonometric logic. What I mean is I need a shape that makes perfect sense before there’s any point in finding the equations describing it. If I already know that it’s a simplification, any equation derived from it will have limited use.
Again, I think I won’t bore you with the examples of minor errors in the previous shape. However, when I turned the shape around and looked at it closely, there were still some illogical steps. Perhaps this time I’ll show the polished version and let you see whether you’re able to spot the differences to the last post.
Here is the y-z projection:

And here the x-y projection:
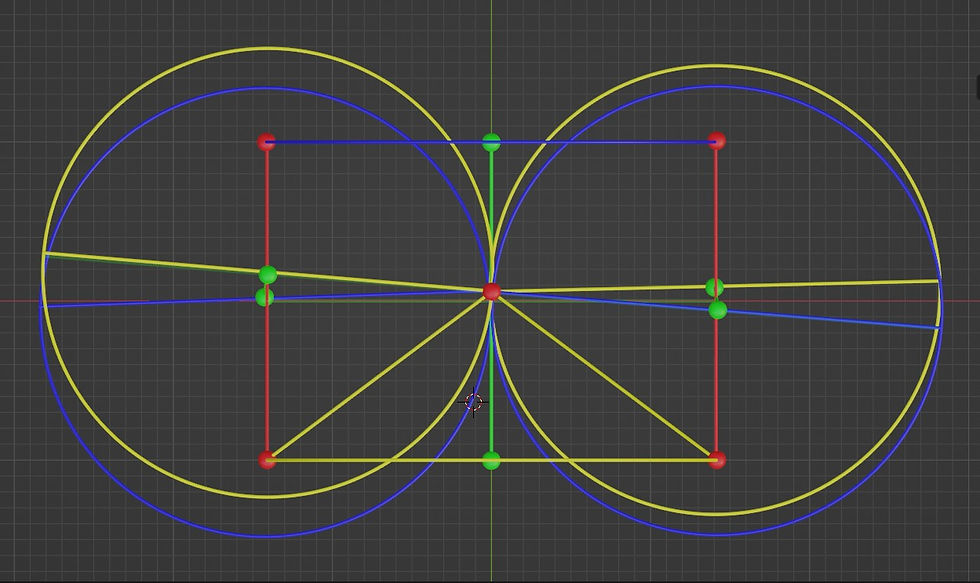
And the y-z projection:
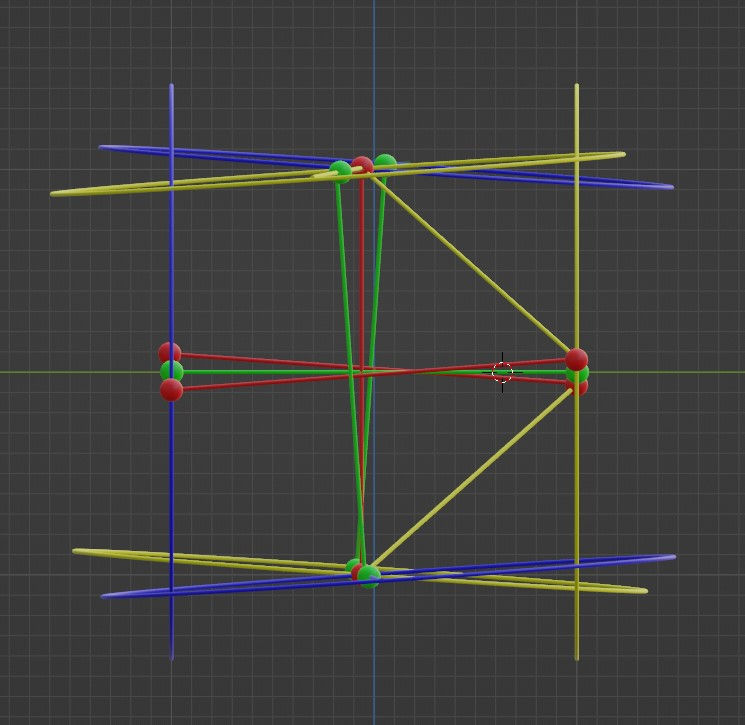
And finally, the rotating 3D model:
If I say so myself, I can’t see any obvious errors in this shape any longer. However, because I made clear changes to my previous shape, I’m unable to jump for joy just yet. The probability of finding at least minor errors is still significant.
What I need to do next is to find all of the remaining errors, if there are any. And obviously correct them. At this point I should be able to turn the shape into equations. If the equations are rational, I should be able to reproduce the reflection shape with absolute precision. Once this is done, the equations should be usable to determine what kind of twisting and bending this complex interplay of reflection produces. In the best case scenario, I can verify the main mathematics of the reflection theory in the next few days.




Comments