Theory of Everything for Dummies
- Kalle Lintinen
- Aug 23, 2023
- 14 min read
While I could be working on honing my manuscript for the Theory of Everything, I decided to take a small break and instead of writing the theory in complicated science and math jargon, I’d try to explain it so even a kid could understand it. But without simplifying it and avoiding ‘lies to children’.
So here we go:
Theory of Everything for Dummies
1. A Long Foreword
What’s is matter? This simple question is the most profound question of all and up to just about now, not properly answered. We’ve known, thanks to Albert Einstein, that energy and matter are connected with the equation . In this equation E is energy, whose basic unit is a joule (J), m is mass, whose basic unit is a kilogram (kg) and c is the speed of light, measured in meters per second (m/s). So, what then is energy? Wise people try to explain energy with a sentence:
In physics, energy is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat and light.
What I say about the above sentence is that the emperor has no clothes. The sentence is a fancy way of saying “I don’t know what energy is, but I know what it does and how it behaves”.
The theory of everything is a better sentence to explain energy. This is what I say what energy is:
Energy is a countable number of spherical elementary particles that are present as strings moving at the speed of light.
I’d be tempted to explain more about energy, but really the above sentence is enough. This might sound complete. How on earth can this simple sentence convey all necessary information about energy? The reason is that there is nothing else in the physical world apart from these spherical particles of energy that move at the speed of light. No truly fundamental forces, no truly elementary particles of matter and even space-time is just space and time.
But you’ve heard a million times that there are fundamental forces and fundamental particles. You might ask “do you think fundamental forces and elementary particles don’t exist?” My answer is that sure there are fundamental forces and elementary particles, but the key is the word ‘truly’. If you define them as interactions that do not appear to be reducible to more basic interactions, the key in this sentence is ‘appear’. Without the knowledge of the elementary particle of energy, there appears to be no interaction that explains fundamental forces. The same applies to elementary particles, that are said not to be composed of other particles.
I’ve found that both light and matter (and antimatter) are made of strings of spherical particles of energy, each of which move at the speed of light. What this means is that naturally elementary particles (of matter) are also made of these. This idea could have been thought by anybody who looked a bit more closely at , and probably many amateurs have. But us scientists have been taught to know better. We’ve been taught this fancy concept called wave-particle duality. We’ve been taught that light is both a particle and a wave. The problem is that while this sentence is true, it’s a bit like saying a car is both metal and a vehicle. Both of these are true, a car is made of metal and it is also a vehicle. But to say a car is metal is obviously wrong. Being made of metal is not the same thing as being metal. But this is what we’ve believed for over a century. We’ve believed that light isn’t made of particles, but that itself is a particle.
So, why do we believe that something that is a wave is not made of particles? Because we’ve never detected that light could be split into something other than light. And if you can’t split light into something other than light, how could it be made of something else?
But a much bigger problem is that experimental evidence seems to disprove the existence of an elementary particle of energy. You might have heard that the smaller the wavelength of light is, the higher its energy. This is a bit hard to explain without going into fancy scientist talk, but it basically means that the smaller the particle of light is, the more energy it has. It’s like describing a blue whale as a weakling and a fly as a superhero. That is, a quantum of light that is extremely small, a gamma ray has much more energy than a quantum of light that is extremely large, a radio wave.
This is actually the clue that finally led me to the discovery of the theory of everything. You see, I’m a chemist and deal with molecules and not a physicist who deals with forces. In my everyday life I can pretty much ignore forces. They play absolutely no part in the working life of most chemists. But what I can’t ignore is the interaction of light with molecules. We chemists use all kinds of light to probe the properties of molecules: especially (but not limited to) ultraviolet, visible and infrared light. This field of study is called optical spectroscopy. Very simply put, we take a material and shine light onto it and depending on what changes there are to the light, we can deduce what the material is made of and what is happening in the material. To explain in any more detail, I will probably loose too many readers, so I’ll try to simplify what kinds of things can be seen spectroscopically.
One slightly less common spectroscopic instrument is a dynamic light scattering (or DLS) instrument. It shines laser light into a dispersion (particles in liquid). If there are particles that are larger than a single molecule, the laser light will scatter from them, and the size of the particles can be determined from the scattered light. This is an instrument which I’m extremely familiar with, as I used it for my master’s thesis twenty years ago, and have been using it if not ever since, at least for the past nine years, and many days for the duration of the whole workday.
The first inklings of the discovery came from me observing that the spherical lignin particles that I work with seemed to behave extremely predictably in mixtures of water and alcohol, but predictably in an unexplainable way. To shorten a very long story, my spherical lignin particles were rather small, about 200 nanometers (nm) when I measured how light scattered from them in water. But if I added ethanol to the dispersion, the particles swelled. With very low ethanol concentrations, the swelling seemed to be roughly proportional to the ethanol concentration, but as I increased the ethanol concentration, I saw unexplainable jumps in the size at very specific ratios of ethanol and water. Below is an actual graph, where each of the dots is the result of at least one experiment. And the dots that looked way too big, I replicated so that I was sure that it wasn’t just about random noise.
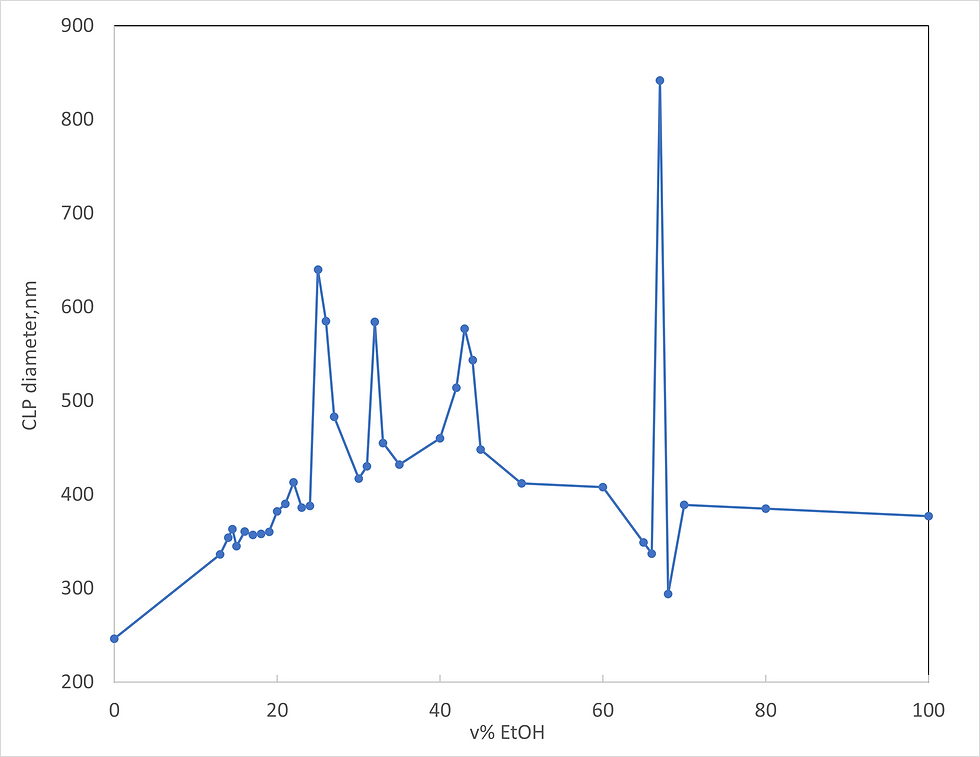
At this point I didn’t have a good idea of the interconnectedness of all molecules, but I already had a very strong hypothesis that this was the case with lignin. You see, I had realized during the early months of the Covid-19 shutdown that lignin, the second most abundant biopolymer (at least on land) after cellulose must be present in all plants with fibrous structure as hollow nanotubules. I even managed to image them as such in electron microscopy, as you might interpret from the image below.

But the problem was that my hypothesis required there to be some force that keeps molecules interconnected in a way that allows the assumption of lignin being present as nanotubules. For a long time, I just ignored the deeper physical theory behind this and assumed that intermolecular forces, such as hydrogen bonding and Van der Waals bonding are enough to explain my findings.
The first clue to the theory of everything came when I was thinking about my experimental data and considered “what if my hypothesis of supramolecular structures doesn’t just apply to lignin, but also to water and solvents?” And this started the ball rolling.
Again, skipping a lot of the details, I asked myself “what if the absorption peaks of water are not just some abstract numbers relating to vibrations, but relate to the size of supramolecular water and the size of light?” And this was it! A very simple sounding question that anyone could have posed, and probably already had. But the key was that while everyone else who was otherwise scientifically literate that light couldn’t be a physical ring, I allowed myself to consider this option.
If light was a ring and liquid water were supramolecular sphere, how would this look like? First of all, not all wavelengths of light would be equally absorbed by water, but if water were spheres of a very specific size, then it would preferentially absorb rings of light of these specific diameters, as these would be more readily stopped by the spheres of water of this particular size.
What else? If there were only spheres of water of one size, there would be lots of free space between the spheres. So, there would probably be smaller spheres (or other shapes) of water between these larger spheres. And if water was present as spheres, their thermal motion (movement by heat) could not be random but would rather be rotating. And if you have spheres rotating against each other, there must be friction. And if there’s friction, something could be detached in this grinding motion. And this something would be protons, which is detectable as the pH of water.
Next, I continued by thought experiment and assumed that it isn’t large spheres of water grinding against each other that release protons, but the grinding of the smaller spheres (or other shapes) grinding against these larger spheres. And this would mean that the density of water would be linearly correlated with the proton concentration of water.
And lo and behold: I went to look at the table that showed the density of water as a function of temperature and then at the table of the proton concentration (actually pKw) of water at different temperatures and I was able to make a plot that’s both linear and not found anywhere. It appears that no one either had thought to make this plot, or if they had, they didn’t think it was a sufficiently important discovery to publish it anywhere.

So armed with this discovery I began frantically gathering more and more data on the properties of water and its absorption spectrum, as well as anything else that I could use to test my hypothesis against.
And this is about the same time when I realized that the ring of light sounds like a string of the string theory. But not quite. While string theory is the current best candidate for the theory of everything, it requires there to be plenty of extra dimensions besides the three spatial dimensions and time. But what I realized is that molecules must be made of the same types of strings as light: ones moving at the speed of light and not vibrating in extra dimensions.
The problem, however, was that the physics and mathematics of string theory were so alien to me that I couldn’t even compare my theory with the different versions of string theory. So, I tried to write a manuscript almost without addressing the mathematics at all. I just made rather passing remarks about the logic of the supramolecular shell allowing for the existence of ring of light larger than a single photon and of the existence of a particle that is extremely small and moving at the speed of light.
Almost exactly one year ago, after a lot of wrangling with different journals, I got my manuscript for peer review in Scientific Reports. But after an excruciating wait of about four months, I received reviewer comments that my manuscript was poorly written, and the reviewers didn’t really get what I was saying.
The annoying thing was that even though they had probably misunderstood what I was saying, they were probably also right. The manuscript was poorly written because one year ago I only had a very rough hunch about what I had discovered. So, I decided to go back to the manuscript and try to really answer the questions the reviewers had raised. And after about eight months I can say I didn’t know squat back when I wrote the first paper. While the core of the theory remains intact, the theory didn’t have a solid mathematical core. And the only people who are allowed to speculate are those who use proper mathematical tools for this. But with enough determination I was able to build this core. It wasn’t easy while working on it, but once I figured things out, everything became blindingly obvious.
So here is the theory of everything in a nutshell:
2. The Theory of everything in a nutshell
As incredible as it might sound, the theory of everything is the sentence:
“There are only spherical elementary particles of energy that move at the speed of light.”
I might expand it to:
“There are only spherical elementary particles of energy with a radius of Planck length that move at the speed of light .”
But then I might not be telling the truth. The elementary particles of energy surely have constant radius, but whether this is Planck length or something else. Why I mention the Planck length is that in the mathematical analysis of String theory, it is believed that the strings that vibrate in ten dimensions would be of this size. However, I haven’t encountered the Planck length in my analysis, so I won’t make further comments on it.
So, what about everything else in the universe? As far as my analysis goes, there is nothing else in the physical universe. No other particles and no forces that act without physical contact. What this means is that all of the elementary particles, light and antimatter are all made of the elementary particles of energy. And while I don’t yet have a mathematical description of how the elementary particles of energy do it, they are the cause of fundamental interactions. And the exact phenomenon from which the fundamental interactions stem from is refraction.
What this means is that refraction is both something very different from what the current story tells it to be, but at the same time exactly what the mathematics of refraction says. While this might sound problematic, it really isn’t. We humans are extraordinary storytellers and can weave stories that convince most people. Especially if the story is backed by mathematics.
The only thing we really need to know is how light behaves in any substance other than a vacuum. We know that in vacuum light moves at the speed of light. However, when light moves through anything other than vacuum (mostly in gas, liquid and solid), the speed of light is slowed down. I’ll just ignore the current explanation and say what my theory says of light:
Light is a ring of spherical elementary particles of energy (Figure 1 b, yellow ring) that stretches into a helix (Figure 1 d, yellow helix) when it collides with matter. And the higher the refractive index of the matter is, the more the helix stretches. Because the elementary particles of energy always move at the speed of light, their collision with matter cannot convert their energy into something else. Rather, the collision causes each of the particles in the ring to move in a helical path (Figure 1 d, black helical arrow), rather than in a straight line as in vacuum (Figure 1 b, black straight arrow). While this might be obvious for some, the movement of the elementary particles of energy now have a linear component and a rotational component. Really, there is only one movement, but it is a useful mathematical trick to separate these two components in two.
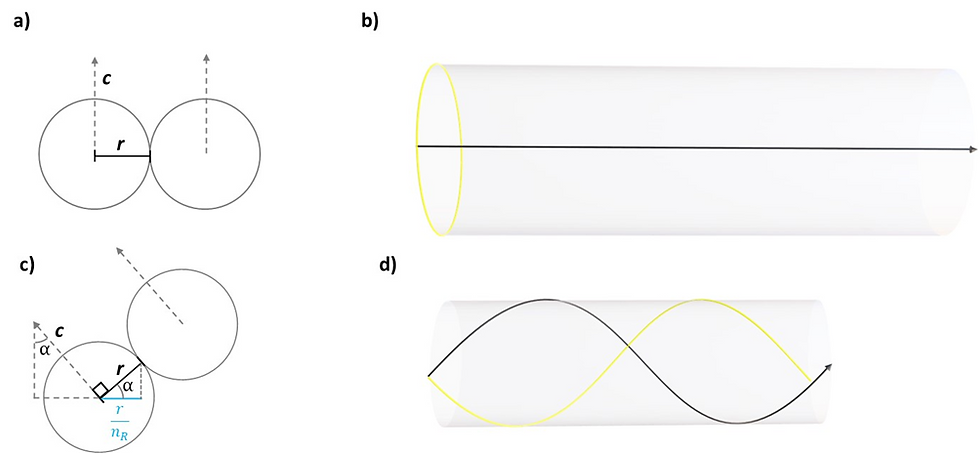
Figure 1. Light is a ring that stretches into a helix.
If I wanted to be very simple, Figure 1 would already be everything you needed to know about the properties of these elementary particles. The only annoying thing is that Figure 1 says nothing about how these elementary particles are arranged in matter.
But fear not. I’ve figure out what happens in matter. The same refraction that causes the elementary particles of energy to move in helical path causes them to be trapped into a toroidal orbit, when several helices of these particles are entangled.
This sounds extremely complicated, you might say. But it really isn’t. You can consider an infinitely long ring of spherical elementary particles with a miniscule rotational component versus the linear component. This means that once the elementary particles have orbited one turn around a toroidal path, they aren’t yet at the place where the started from, but on the opposite side of the small ring of the torus. But place where they started from isn’t empty. It still has another elementary particle on it with exactly the same orbit as the original one. However, once the elementary particle has orbited a second turn around the toroidal path it finally is where it started from.
But this cannot be possible if there aren’t elementary particles with a phase-shifted orbit orbiting the same toroidal path. This sentence is quite complicated, but in real life it just means that there are four orbits that are each separated by ninety degrees. The collisions of these four orbits are enough to keep the elementary particles in near-infinite orbit. But the trick here is that as there are four entangled orbits, the orbit has to be two separate circular loops.
If you use abstraction and portray the distance between elementary particles as vectors and draw their path in space as helical tori (or toruses), it is possible to visualize their interconnectedness. However, as soon as you begin to make abstractions, you lose touch with what is really going on.
Figure 2 a shows the elementary particles both as vectors and as circles in three different 2D projections of the 3D reality. In Figure 2 b, to see what is going on in ‘real life’ the four orbitals of elementary particles are visualized in four colors. Here it is most clear to see that none of the elementary particles touch other elementary particles in the same orbit, but rather those in the neighboring orbits. Win Figure 2 c we see the abstraction, which is crucial for the mathematics, but useless in getting an intuition of how the particles touch.

Figure 2. Matter is more than one helix that entangle into a closed loop.
But Figure 2 isn’t good enough as it is. Matter doesn’t float in space as entangled double-loops. Rather while following the same mathematical principles as Figure 2, matter must be made of multiple loops. We know that charged particles are experimentally observed to be extremely spherical. So how do we take the shape from Figure 2 and make it a sphere? We increase the number of loops and the twist the loop around its axis, as shown in Figures 3 a and b. This is the general shape of electrons and protons.

Figure 3. In charged matter the helix folds over for 720 degrees to form a closed spherical shell.
And how about molecules? Are they spherical as well? No: they are made with a different process. In the formation of a hydrogen molecule, an individual atom is still a double-loop, as depicted in Figure 2, but two double-loops knot to form a bi-spherical structure, made of circular arcs. This is shown in Figure 4.
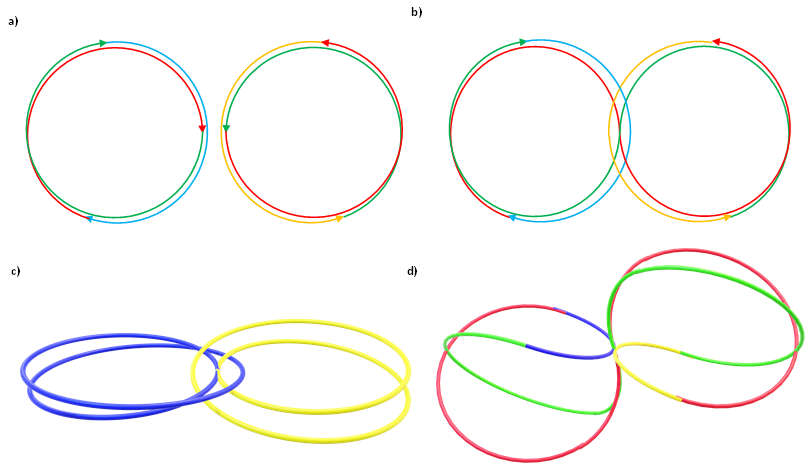
Figure 4. The formation of a hydrogen molecule (H2) knots two double-loops together.
But a single hydrogen molecule isn’t really a thing. You can have single protons and electrons, but hydrogen molecules form supramolecular loops. Figure 5 a to d shows how the elementary particles of energy move in the hydrogen molecule, shown in three different projections. Looking at the figure it is obvious that two orbitals of hydrogen molecules can fuse, to form a supramolecular bond, as shown in Figure 5 e. You might ask, if there was such a bond, wouldn’t we know of it. The comical thing is that we know that to ionize a hydrogen molecule we need to separate its protons and electrons. But we didn’t realize that what is ionized is a supramolecular loop of molecules and not just a single molecule, but a whole loop of molecules. The problem is that thing kind of made sense even without knowing that molecules are interconnected.
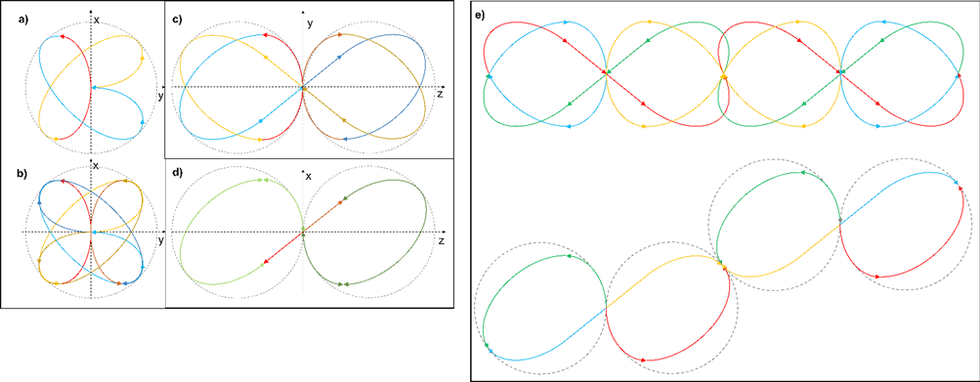
Figure 5. a) to d) The shape of the hydrogen molecule, with circular arced arrows showing the direction of the movement of the elementary particles of energy. e) An illustration of the fusing of two orbitals of hydrogen molecules to form a supramolecular bond.
I could go on with this, but this is the theory in a nutshell. Elementary particles of energy that are refracting from each other and forming helices. I’ve shown a bunch of equations in my manuscript that I can use to depict everything accurately. But as they say in science publishing, every added equation reduces the number of readers. So, this is the theory without a single equation.
3. Objections to this Theory
I wouldn’t be a good scientist, if I didn’t anticipate objections to this theory. While the theory is extremely clear and doesn’t rely on hand-waving, it misses a major point that might be objected to. It doesn’t try to explain fundamental interactions and not really even gravity, even though it at least gets close to that than to the other forces.
I have a feeling that if given enough time, I might come up with a theory of the forces as well. But if I were to attempt to poke that hornet’s nest, I wouldn’t be able to publish anytime soon. So, for now I just hope that the theory will also produce fundamental forces and all sort of other cool things.
However, now the theory is ready enough. I’ll be happy to see how people try to tear it down. I think it won’t break.
And did I manage to write this so that even a kid could understand? Perhaps not any kid, but hopefully a smart kid. The key here is that I've skipped the mathematics that scare people and I've tried to minimize the use of complicated sciencey word if at all possible.
If you wish, you can try to read the theory in science jargon in the manuscript below. It has plenty of equations and terms that most people haven't heard of. But if you feel this post seems far-fetched, the manuscript shows that it's not based on a hunch, but proper mathematics. And physics. And chemistry.




Comments