I thought I was writing a completely different post for today, but I ended up writing about the origami folding of the Higgs boson.
The reason for this detour is that I started out thinking that entangled helices of dots are always very detached. Or more specifically, my initial foray into the origami folding of the entangled helix seemed to indicate that the entanglement of dots doesn’t look like this:
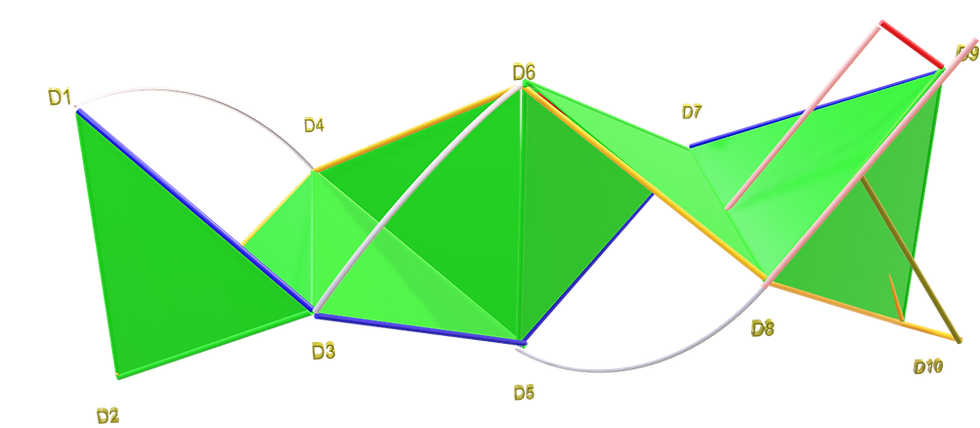
One of the major reasons for this was that when I prepared equations for the above shape, I didn’t seem to get proper circular arcing of the entangled double-helix.
But here’s the rub: I was looking for a circular arc, when in fact the actual shape that I should have looked for is a helix. So, it might be that I was looking at the right solution all along, but I didn’t see it, because I didn’t follow through with the logic. But this is understandable. Without a clear idea of where one is going, the twisting of the structure just looks a bit off.
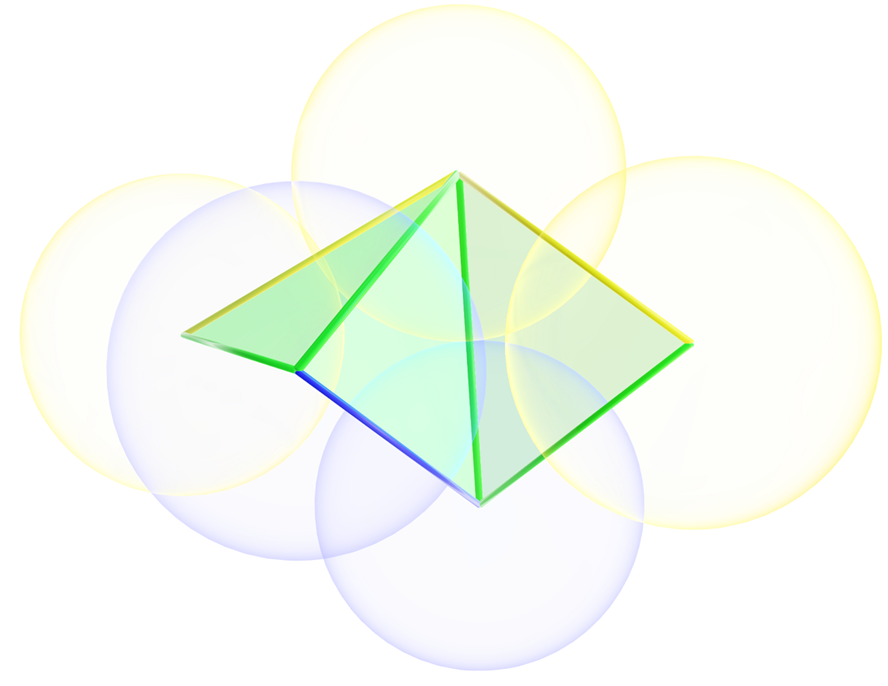
Even here with a small structure, using transparent spheres alongside the triangles it isn’t immediately obvious that the shape is what it’s supposed to be:
But then, if I extend the structure a bit more, I begin to get something that actually begins to look closer to what I’m looking for:
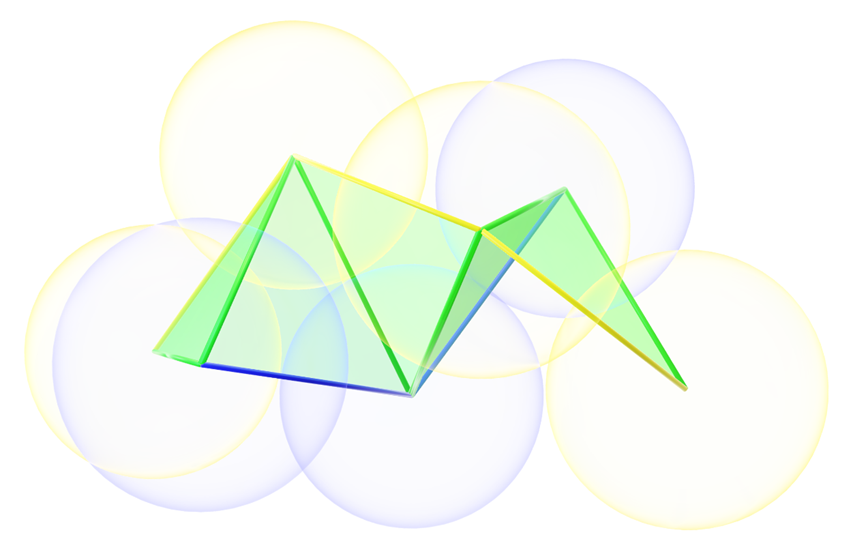
But the shape makes sense only if I know that this is exactly the way it should behave. And even then when I extended the structure even more, the structure wasn’t exactly as I thought it would be:
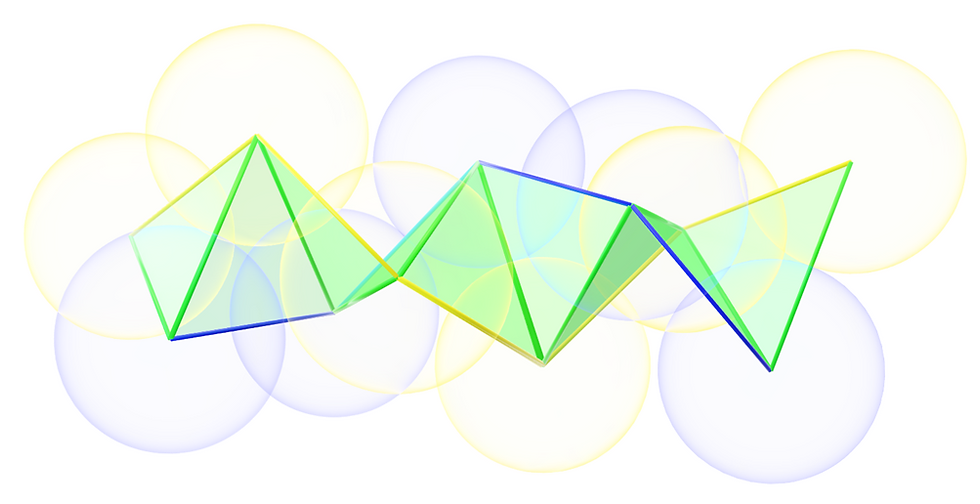
Even with very clear (even strict) rules, this twisted origami structure looks very organic. Looking directly from the front it’s as if there’s no order whatsoever:
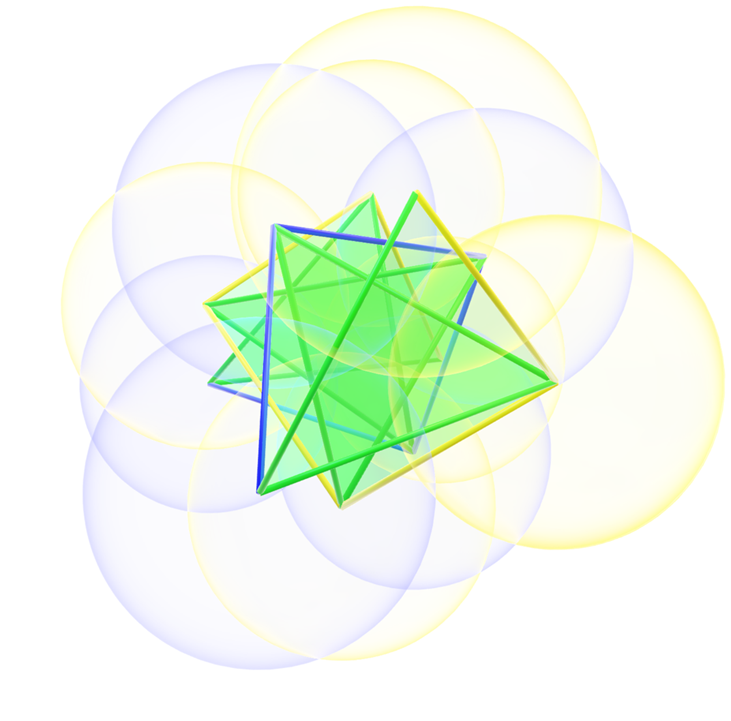
At least for now, I’m relatively confident that I’m on the right track. However, only more work will show whether the logic breaks down or whether this truly is the vectorial representation of the Theory of Everything.
Comments