I had a hunch that life wasn’t plain sailing for the hydrogen orbital. I’ve encountered a rather curious problem. A call this problem a “Perpendicular Zapdos”, due to its slight resemblance to the Pokemon character.
In my last post I showed a jagged butterfly that seemed to replicate the figure that I’d made in Blender with decent accuracy. It seemed there were just minor tweaks left.
But then I went back to the Excel file and attempted to calculate the distance of each dot from its neighbor and got some really funky values. This made me realize that something wasn’t exactly right, but I really couldn’t figure what that something was. Then I realized that I could increase the number of data points and get from a jagged little curve to a pretty helical curve. And this is when I made this:
My Perpendicular Zapdos. For those of you who know Pokemon, there is this one Pokemon, who bears an uncanny resemblance to the figure above. This is Zapdos:
And here is what the curve looks like from the side:
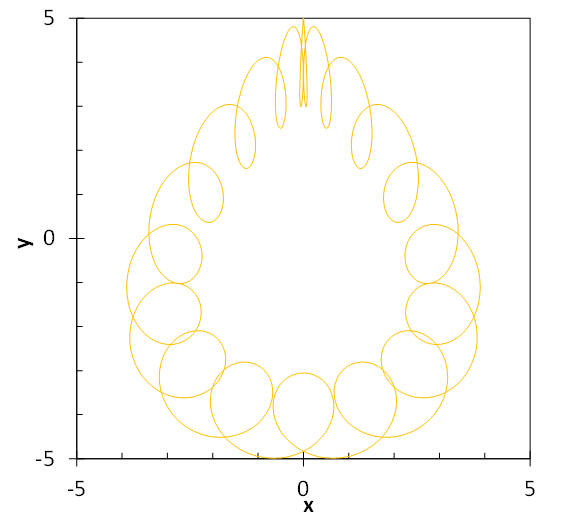
At first it doesn’t look too bad. But then when you look at it closely, you realize that the helices are perpendicular (at right angle) to the direction they should be in. Initially I was very confused, but after some thought, I realized that this is pretty much the same problem that faces quantum mechanics. You can only make the equations work if you use imaginary numbers. To be frank I don’t really understand the mathematics behind quantum mechanics. Not necessarily because couldn’t, but because I’ve never really had to try. Here is a nice Veritasium video explaining imaginary numbers and how they are crucial to quantum mechanics. The video also makes the claim that the imaginary ‘dimension’, or whatever you want to call it, truly exists in the quantum world. However, it seems that I might be on the verge unraveling the mystery of the imaginary numbers in the quantum world.
You see, regular equations describing helices are ok to define the higher level bending of the entangled helix. However, if you try to apply the helical equations to the helical arrangement of dots in uncharged matter, you end up introducing a helix with an identical plane of curving, which is evident in my Perpendicular Zapdos. Instead, what is needed is that this primary helix of dots should be perpendicular to the secondary helix. I don’t yet know exactly what sort of mathematics is required, but I’m pretty sure it involves imaginary numbers.
However, I do need to say that of course I might be wrong. At the moment I’m still relying mostly on intuition. But then again, intuition has got me this far, so I tend to trust it, at least to give me the big picture. For the nitty-gritty details, my intuition can be wrong. To confirm the details I still need mathematics. This is roughly the sort of mathematics that I have to figure out:
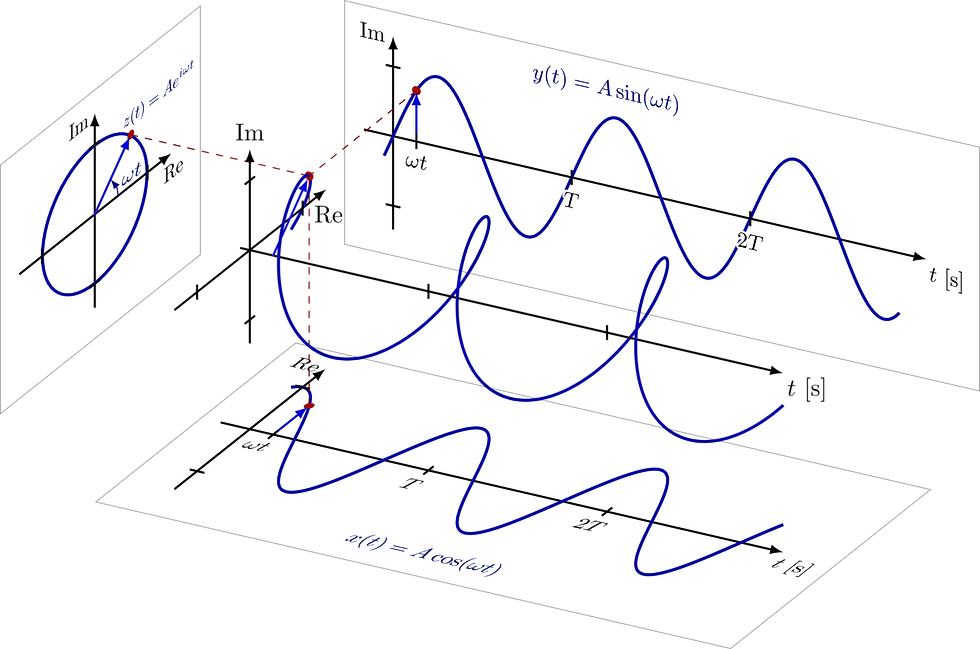
Or to open the figure up, the values of x and y axes are determined with normal sine and cosine, but to get the value of z, we need to raise e to the power of i, where i is the square root of minus one.
Comments