The Most Important Angle(s)
- Kalle Lintinen
- Nov 23, 2024
- 2 min read
I’ve been studying the half a double helix that I presented in my last post for a few days now, I I’ve realized that the shape holds a simple geometric key to understanding the reflection of elementary particles of energy (kaus/dots). And this geometric key is the angle of connection of the kaus at the point of grazing.
This angle is especially visible in the x-z projection below:

The shape consists of two angles on the same tilted plane, where each angle is above 60 degrees, with the sum being above 120 degrees.
Conversely, if one looks at the y-z projection, this angle is completely masked, showing that all four dots taking part in the grazing even are along the same plane.
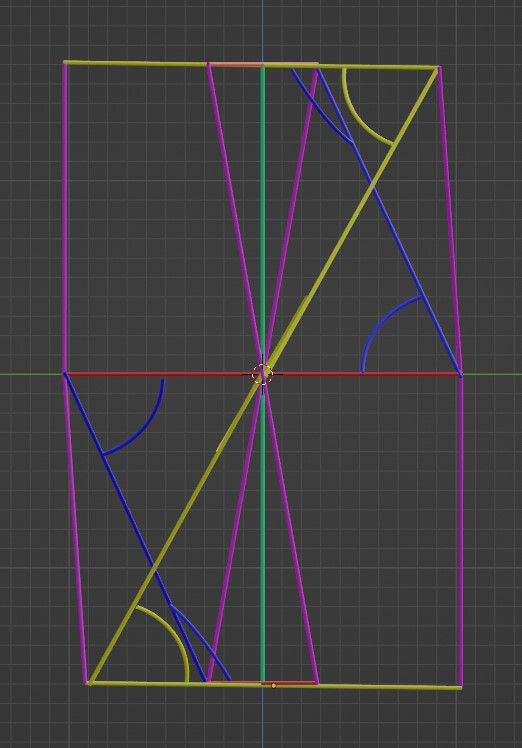
And just for completeness, this is the x-y projection, but I don’t have anything simple to say about it:
And this is the shape in 3D, rotating:
Next, you might be confused about the term angles in the title and the blue angles shown in the above images. Well, that’s sort of an imaginary angle. You see, the red vector doesn’t really show two connected kaus, but rather the shortest path between two neighboring caus. So, the blue angle is between a true connecting vector and an imaginary vector. Because of that, I’m not sure whether this angle is the same is the same as the yellow angle.
Perhaps it’s best to be honest. Even though I think these two angles (which might be the same angle) are the most important angles of all interactions, I don’t yet know how they can be used to derive the equations for the above shape.
But I’m quite confident that just as long as I look at the shape for long enough, it will reveal its secrets to me.




Comments