The Alphabet Soup

In my previous post I talked about all the elements that make up spacetime projections. In this post I decided to spell out what these elements are:

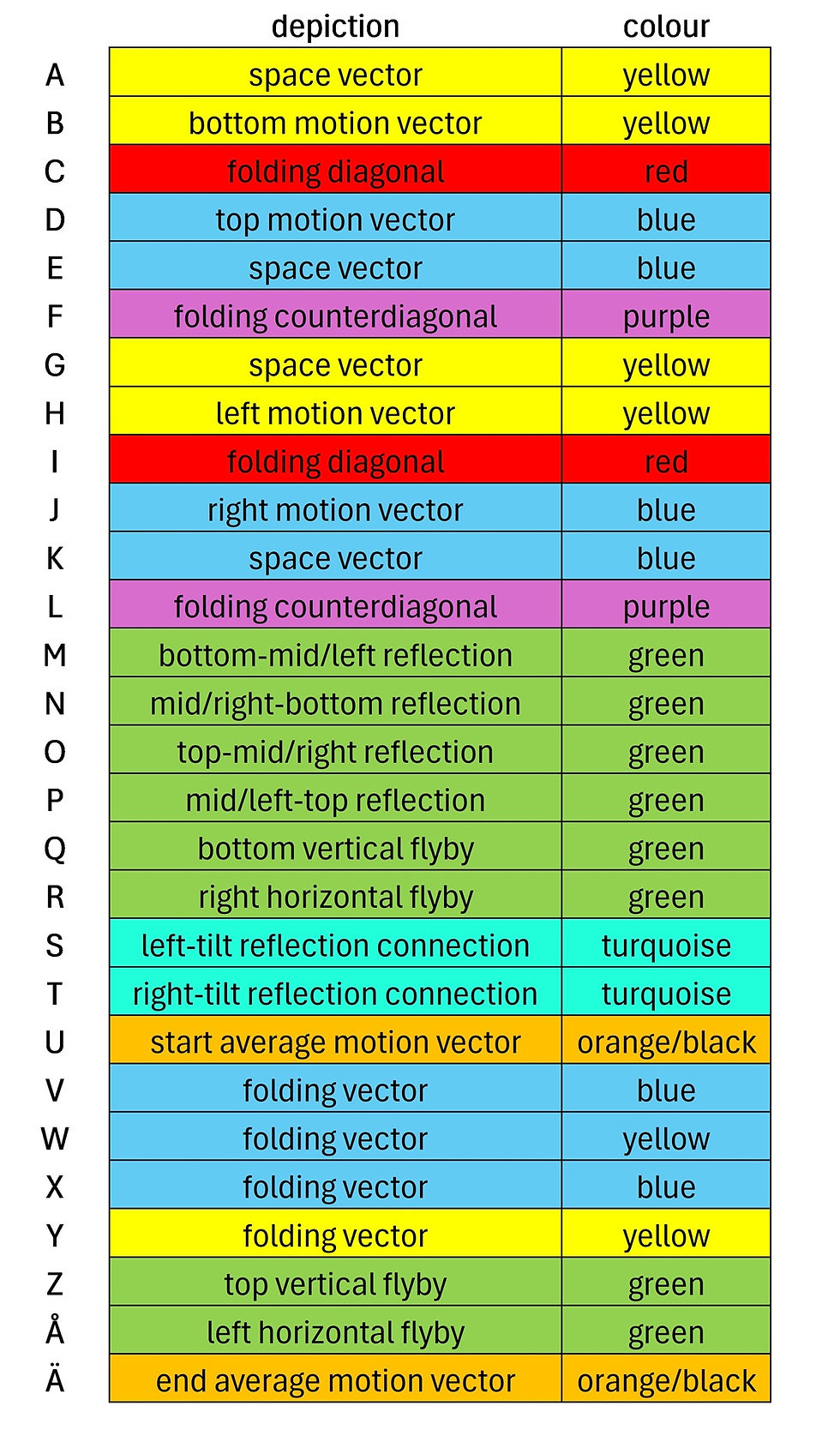
I.e. 28 vectors, each with 3 spatial lengths, as well as 2 spatial coordinates made of 3 numbers. Most of these spatial coordinates are shared with two or more vectors. As you can see, there are more letters than can be found in the English alphabet, so I’ve included letters from the Finnish/Swedish alphabet (which is the same alphabet partly due to historical reasons).

And this is what the letters look like in the three projections:

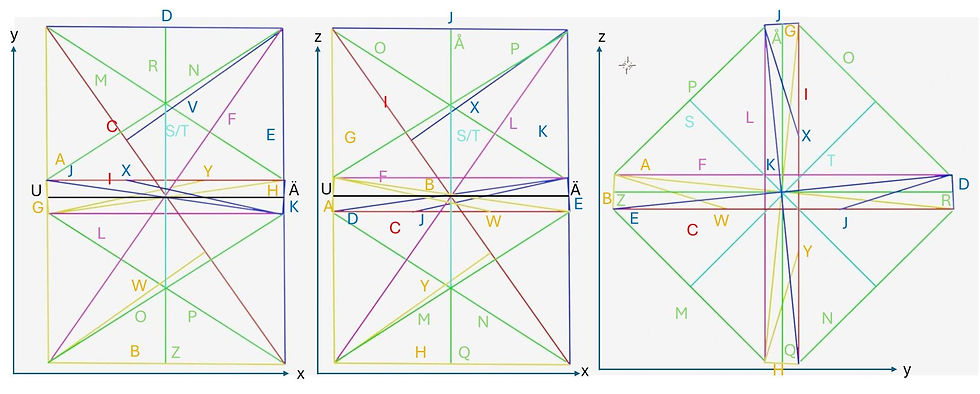
 There are a lot of things going on in the above picture. I think the most notable new thing is that there are four flyby vectors instead of two. You see, if you look closely at the picture, the red folding diagonals must be slightly closer to the center of the unit sphere of reflection than the purple folding counterdiagonal (a name that I’ve ‘invented’, although the term is used with anti-diagonals in matrix algebra).

And this is the model illustrated in 3D, with some rings added:

These rings are important later, when applied to the projections, as they will produces ellipses, instead of just one ring on the y-z plane and a straight line on the other plane.

The shape is way too complicated for me to explain in any more detail in this post. Most of all, because I don’t know the shape too well either. The curious thing is that I didn’t invent the shape, it is more of a result of following logical steps wherever they take me. And oftentimes I’ve started with a roughly correct assumption that serves me well up to a point where I see where its logic fails. In the best case scenario I only need to make minor adjustments, but sometimes I need to scrap the hold assumption.

This time I’m hoping that I don’t need to scrap anything, but only time will tell.