After my last post about the perfect equations for vector refraction, I set about trying to figure out how these equations resulted in a Higgs helix shape instead of a twisted linear rod. One of the problems of the approach was that the equations seemed to produce a twisted helix that was at an angle to the three dots chosen first.
First, I tried to figure out how would the three dots need to be chosen differently. After a bit of trying, I was able to almost get the curves to almost have zero angle. The only problem was that if I attempted to have zero angle in one projection, this produced a relatively high angle in the other projection. In the end, I managed to produce a very small angle. Below you see that with the x-axis being 1800 units long, and the y-axis stretched so that the helical shape is visible, the incline over this length is less than 1/1800, or about 0.03°
However, even then, the entangled dots were perfectly linear to the eye.
Probably roughly at this time, I decided to go back to visualizing refraction once more. After quite a few dead ends, I realized that I need to consider relativistic effects. That is, I would need to think how the dots move, not just how they exist statically in space. In then it hit me, there are two different kinds of refraction, depending on the movement of dots relating to their location. Or more specifically, half the dots touch a dot that is next to them and a dot behind them (relative to their direction of movement), whereas half of the dots touch a dot that is next to them and a dot in front of them. This means that half of the dots experience radically different refractive interactions versus the other half.
This means that on the level of dots, refraction is an asymmetric phenomenon! And who else figured out that the solution to string theory is asymmetricity? It was Sheldon Cooper in the TV series Big Bang Theory. In it, Sheldon realizes that he’s been trying to describe an imperfect world, and the only way to do this is to introduce imperfections into the underlying theory. So instead of supersymmetry, it would be super asymmetry.
While none of the details (of which there aren’t too many in the episode) match with my equations, the premise is the same. I had been trying to describe the two entangled strings of dots with the same equations, assuming that they should be the same. Only when I realized that the equations aren’t the same, I saw the solution.
So, while the equations that I already solved were correct for one half of the dots, I would need different equations for the second half.
This is what the refraction of the second half of the dots (yellow ones) looks like:
The green line ending with a red circle is the non-refracted dot. The red circle describes all of the locations where the refracted dot could be. The yellow sphere at the end of a red line depicts the refracted dot. In this illustration, the angle of refraction is 10°. Besides the green line ending in the place where the yellow dot would be with no refraction, there is also a green line depicting where the next blue dot would be without refraction. If we know where the first yellow dot and the first blue dot are and where the second yellow dot is without refraction, we can use the vector equations from before to determine the second blue dot. To be clear, I use the superscript 0 for zero refraction reference vectors, and the superscript R for the refracted third dot.
Without going too much into details into how I derived them the is the equation for the third dot:
However, this equation does not apply to the fourth dot. Rather, the old equations that I showed two posts back should apply to the fourth dot. And of course, the fifth doth is again described with the same equation as the third dot.
Or this is what I hope will happen once I combine these equations. Again, this is my sort of masochism: I’m revealing my train of thought before I’ve checked whether it’s correct. I’m moderately confident that I’m at least mostly right.
And here is a sort of a cheat, where the refraction is shown to occur in two directions from the same central vector.
The reason why I call it a cheat, is that I should have started with the blue sphere on the left and define the central yellow sphere based on that, instead of vice versa. However, this 'cheat' allow me to compare this new figure with the old figure of refraction.
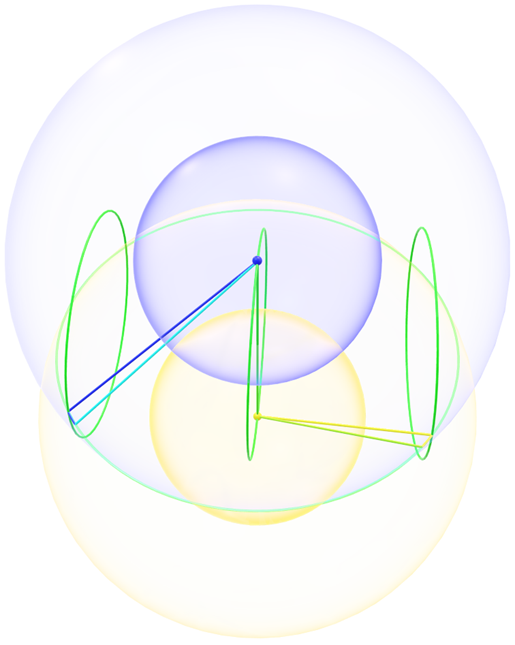
While the above shape is similar to the new one, clear differences can be observed as well. Hopefully I'll be able to post more on this in the near future.
Comments