Reinventing Calculus
- Kalle Lintinen
- May 15, 2024
- 3 min read
It’s been quite a while since I last posted. The reason for this is pretty obvious for all of you who’ve been reading my posts. I’ve once again tried to solve mathematical problems. And they take time.
While I haven’t yet fully solved all of the problems relating to how reflection can be best expressed mathematically, I’m getting extremely close.
You might remember the saint Hannes knot equations that depict the location of the elementary particles of energy (dots):
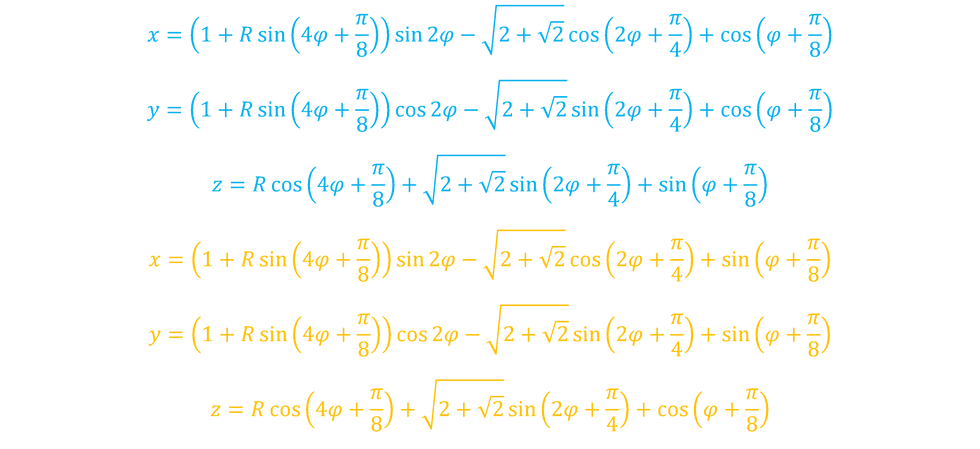
However, these equations are sort of static. Granted, when the term φ is changed from zero to 2π, you get the location of dots at any point in time. But the equations themselves do not describe the movement of the dots.
For their movement, I need to reinvent calculus. According to Wikipedia:
Calculus is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
So, if the above equation describes geometry, we need to introduce continuous change to the geometry. But what is this change? The change must be the true nature of the movement of dots. What I’ve been figuring out has been the integral of the movement of the dots. I’ve had a rough idea of this for a while, but only when I tried to match the movement of the dots to the above equations, did I realize this.
You see, the z term in the equations should describe the location of the dots along the path of the movement dots. Except, the sines and cosines in the above equations are still a bit off, because I didn’t properly realize what they were about. You see, cosine indicates the parallel movement of dots and sine indicates their reflection, or the continuous change of calculus.
This means that the derivative of the z equations should describe the parallel movement of dots. This means that all of the terms should be cosines in the derivative and sines in the geometric equations.
What this also means is that the x and y equations both describe reflection. This means that the sum of the geometric equations should only consist of cosines. This means that their derivatives should (mostly) be sines.
Because I’m still not ready with the equations, I won’t bore you with the details. But I have something better. You have possibly heard that Isaac Newton invented calculus (at the same time as Leibniz) to explain celestial mechanics. However, Newton couldn’t really explain what made the celestial bodies follow his mathematics. He got quite far with his laws of motion, though:
1. A body remains at rest, or in motion at a constant speed in a straight line, except insofar as it is acted upon by a force.
2. At any instant of time, the net force on a body is equal to the body's acceleration multiplied by its mass or, equivalently, the rate at which the body's momentum is changing with time.
3. If two bodies exert forces on each other, these forces have the same magnitude but opposite directions.
These laws aren’t bad at all. However, when applied to dots, the first law of motion is very unhelpful. Dots are always acted upon by other dots. And what the action is, isn’t really a force, but a reflection.
The second law is interesting, but not very descriptive of dots. In an equilibrium orbital, each dot experiences relative negative acceleration because of reflection. How this translates to force, I have yet to figure.
The third law is the basis of reflection. When two dots collide, the forces they experience must be equal, which means that the angle of reflection must remain constant.
Unfortunately, I cannot reinvent all of calculus in one post. It will take some time for me to be able convert reflection to calculus, but I’m confident that I’ll be able to make serious progress in the near future.





Comments