Reflection Cymbals
- Kalle Lintinen
- Oct 5, 2024
- 2 min read
In my last post on my quest to explain the Theory of Everything with the reflection of elementary particles of energy (dots), I talked about completely rebuilding the reflection model of dots based on a tilted reflection tetracones.
This tilting allowed me to handle the geometry of reflection accurately, where the older models placed two of the six dots in the model into the wrong place. Based on this more accurate model, I’ve tried to check the accuracy of the model by stacking several shapes up and see whether the stacked models fit seamlessly.
I was about to talk about stacking in this post but realized something more fundamental in the process. I realized that while there is nothing exactly wrong with the reflection tetracone, there is an even better mathematical tool to describe reflection. This time I call it a cymbal of reflection. And because the shape is so cool, I’ll show the rotating 3D model before the projection:
While it might appear from the video, that the two brass-colored round shapes are flat discs, they are indeed cones with an extremely small depth. Because these two cones are shallow and facing each other, I call the cymbals and have even colored them with the color of a Zildjan cymbal. Or to be more precise, two opposing cymbals would be hi-hats, but I like the word cymbal better.
To illustrate the concept of the cymbal of reflection, let’s look at the y-z projection. It almost doesn’t show the cymbal shape, as the cone is so shallow, but when the cone is drawn inside a relatively large green sphere of reflection, the idea hopefully becomes clear(er). The sphere has a radius of the flight path of a dot between two reflections. This means that you can fit a grazing ring into the sphere where one end of the ring touches the center and the other end touches the surface of the sphere.

And the cymbal shape is best observed in the x-y projection:
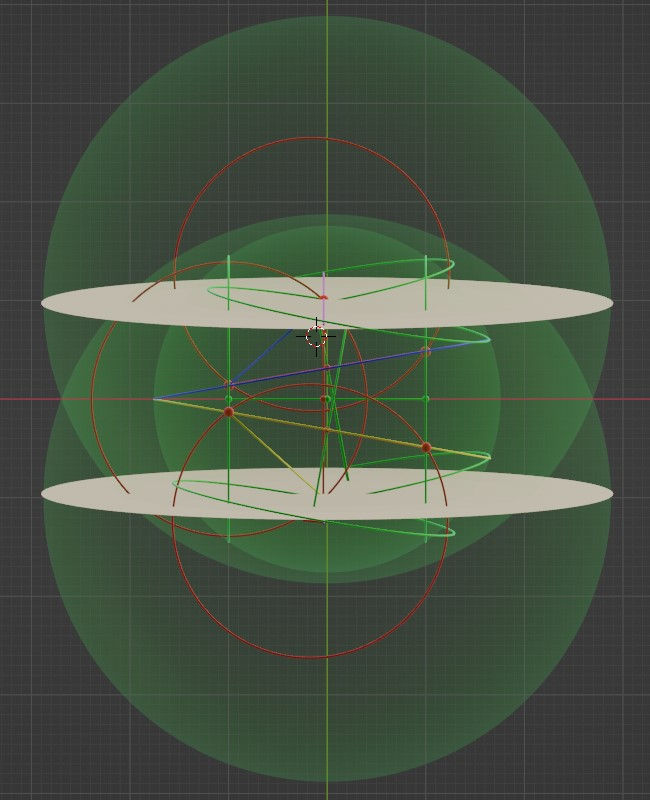
And I have to show the x-z projection for completeness, even though I’m not sure it will that helpful for you, dear reader. Well, at least it shows the two grazing rings, one on top of the other.

So, what next? If this model is 100 % correct, I should be able to transfer the shape into equations that should allow me to transfer the shape to Excel and enable be to stack however many of them on top of one another. And if I can, this would mean that this would be the foundation of all physical interactions. Which in turn would mean that I could finally write the darn “Theory of Everything” -manuscript that I’ve been working on for over two and a half years.
But I’ve been here before. Perhaps not as confident as now, but still relatively sure that I’ve figured it all out. Because I know how easy it is to fool oneself, I’m still trying to keep it cool. However, it does seem highly likely that there aren’t any major obstacles left. This is juust the sort of thing to say just before hitting a brick wall, though…




Comments