In my last post I talked about having the tools to test ideas about helical twisting and showed some cool images. However, I didn’t really address how refraction is depicted between dots. So, I knew this was something I needed to do before really being able to do any mathematics.
Armed with my knowledge of Blender, I started just fooling around and trying to figure out what made sense visually. To begin with I assumed linear refraction. That is, while the angle between three dots without refraction is 60 degrees, if you have refraction, you just increase the angle from 60 degrees to a higher value, like this:
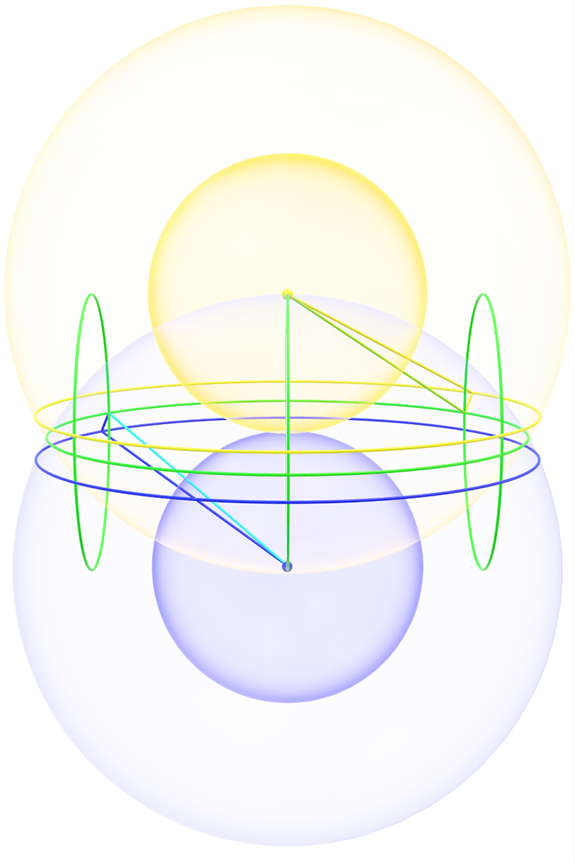
This seemed like a feasible idea, so I tried to see how these shapes would stack up. The results weren’t very promising:
But for a couple of hours, I didn’t even realize that I had made a mistake. Or to be precise, I had made two. The first mistake is a bit harder to explain. It relates to the refraction being stepwise, where the helix sort of folds first to one direction and then to another. Once I have proper images to explain this, I’ll explain this phenomenon in another post. However, the easier mistake to explain is that refraction isn’t linear, but orthogonal.
While the term orthogonal refraction sound complicated, it isn’t that at all. It’s pretty much the same concept as in the spring of a mousetrap. You have two rigid rods attached to a spring, which is at a specific angle without a force that pries them apart. When you apply force, you can stretch the rods from their equilibrium. This is (sort of) what happens with dots:
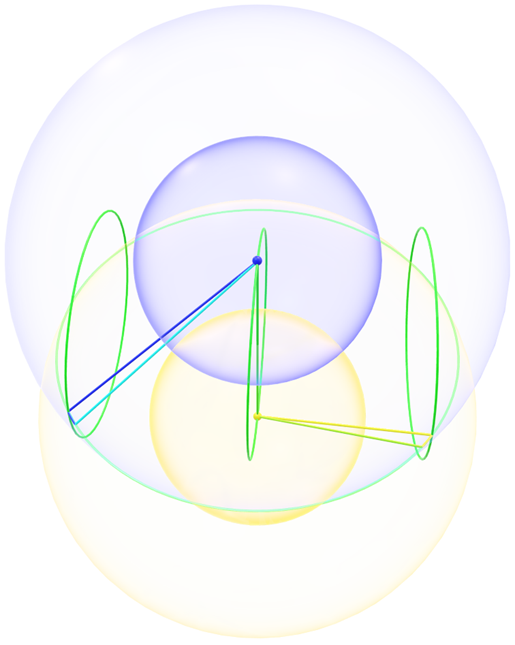
From the picture above it might not be obvious, but this stretching inevitably causes otherwise linear entangled helix to bend. When viewed from above, this bending is more pronounced. In the image, the green-yellow and turquoise rods depict the state without refraction and the yellow and blue rods depict the refracted state.
The comical thing is that I had already sort of known this a while back, but my skills in Blender were not yet good enough to test the idea.
However, this isn’t the final solution yet. Next, I need to make sure that the refracted dots really stack up to something more presentable than the mess shown for the linear refraction. If I manage to do this, then I just might have the courage to go back to equations.
Comentários