More Reflection Rings
- Kalle Lintinen
- Oct 1, 2024
- 3 min read
In my last post on my quest to explain the Theory of Everything with the reflection of elementary particles of energy (dots), I talked about wonky grazing rings. These grazing rings depict all the possible paths that dots can take that pass a specific point of grazing. At this point of grazing, there is no distance between the two dots, but because they move on two separate parallel plains, they never encounter each other.
Based on this concept (and the rest of the mathematical tools I’ve devised), I’m building a completely different way of thinking about reflection. In this post, I’ll introduce a sneak peek into it.
At first, let’s look at the x-y projection of the reflection model, with a significant number of elements from previous models hidden. The main elements left are the two circular planes of reflection, depicted with blue and yellow lines at angle from the horizontal line. On either plane, one can see two red spheres, depicting the starting and ending point of dots between reflections. There are two green vertical lines through pairs of dots, depicting the x-y projection of the grazing ring depicted in the previous post. Both the circular planes and the grazing rings are drawn around the same sphere of reflection. If the angle between the two circular planes of reflection were zero, this sphere would have a radius of √2 times the radius of a dot (√2r). The horizontal green line is the distance of the two dots at the point of grazing, whose length must be 2r by definition.
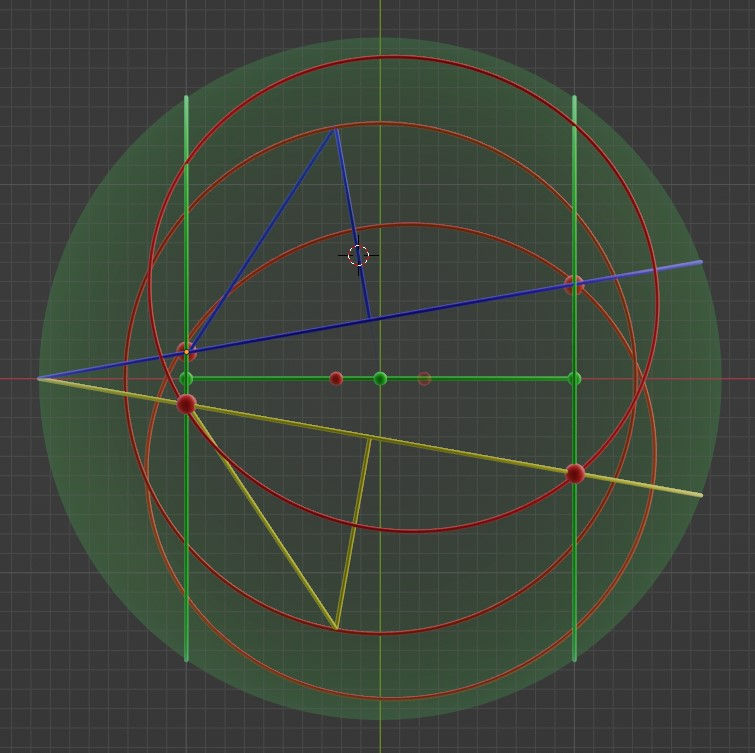
Besides these, there are also ‘more diagonal’ (closer to 45-degree angle) blue and yellow lines, depicting the point of reflection between two blue and two yellow dots. The length of this line in 3D is 2r, again by definition, but in the line in the x-y projection is obviously shorter. As the circular planes of reflection define the location of the reflected dot in relation to the central dot, the lengths of the tilted near-vertical blue and yellow lines is r by definition. This might not be obvious to you, the reader, but trust me on this.
And the final elements in the above projection are the three red rings of reflection. The rings are always of the same radius and are always drawn so that both a blue and a yellow dot are located along the ring. This means that the blue and yellow diagonal dot-connection lines also connect the three rings together.
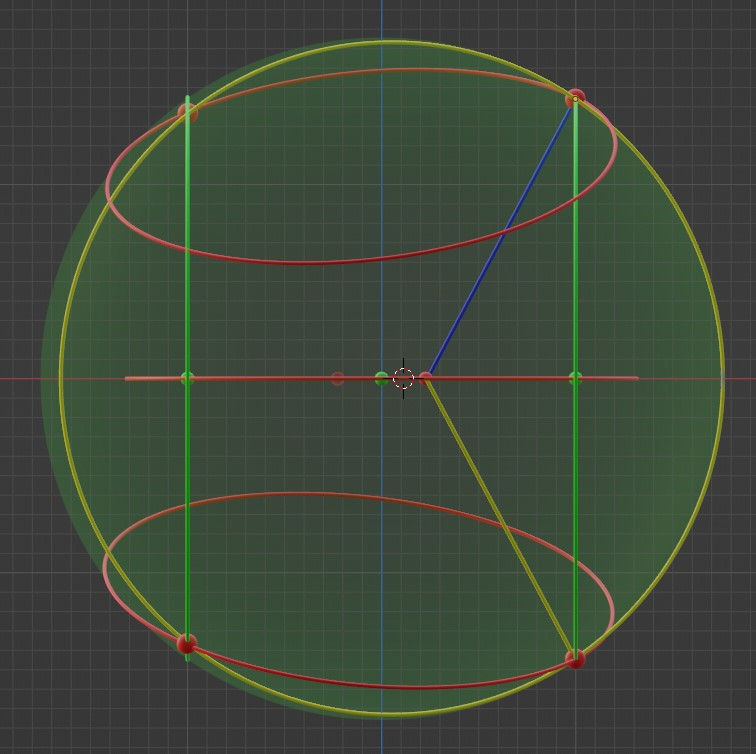
This connection is probably best seen in the x-z projection:
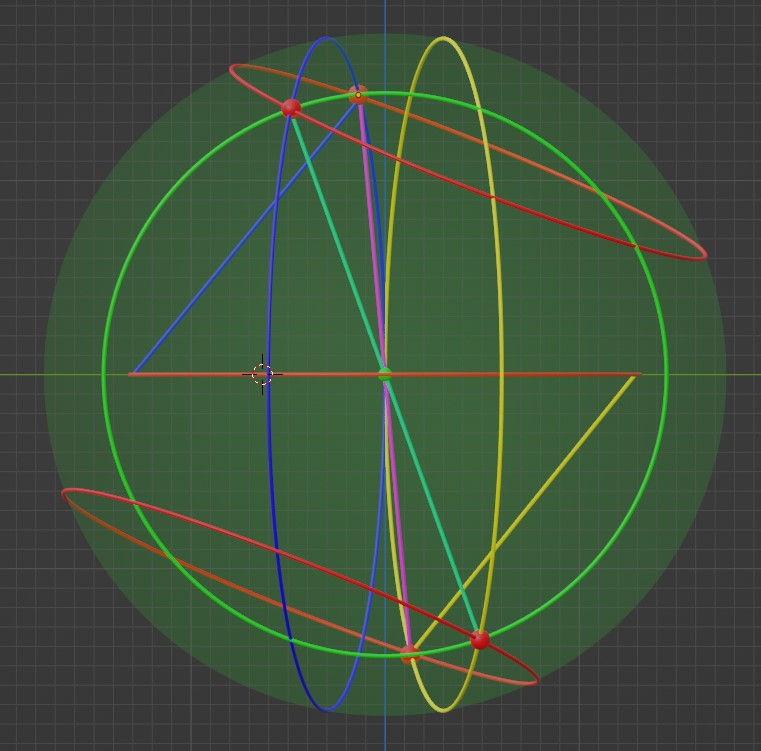
As well as in the y-z projection:
And as always, this is the model rotating:
And if I understand it correctly, the geometry of this model is precise. However, despite the precision, the model is also ‘wrong’, or at least misleading. The reason is that the angle between the two circular planes of reflection is way too large. To get accurate geometry overall, this angle should be reduced to a tiny value. However, the above shape allows me to figure out the equations behind the shape, which in turn should allow me to check whether the overall geometry become sensible when the angle is reduced to a value close to zero.
I hope this will sort things out. Or if I find a contradiction in the model, I’ll know I need to dig deeper to find the faults in this model. If I had to guess, I’d say it’s slightly more likely that the above shape is correct and that things will be solved just by reducing the angle. But I can’t be certain until I’ve checked the math.




Comments