Misunderstanding Mathematics
- Kalle Lintinen
- Jul 2, 2023
- 9 min read
In my last post I talked about the geometry of everything. In it I mentioned that I hadn’t figured out the mathematics out just yet, but at least I had the geometry sorted out to derive the necessary equations.
In today’s post I’m not talking about the equations just yet, but I’m going to talk about misunderstanding mathematics. Mathematics is very accurate as a discipline. The only prerequisite for accuracy are accurate basic assumptions, or postulates. I’ve talked about their importance before, but now that I’m finally approaching the mathematics of the theory of everything, it’s important to talk about the shortcuts that have been made before, which have resulted in very shoddy mathematics. But because the equations have sufficiently accurately described natural phenomena, very few people questioned the validity of the mathematical approach to get to these results. Well, in fact there have been quite a few people to do this, most notably Einstein himself. However, the consensus between contemporary physicists has been that the world is a weird place that cannot be described by anything mathematically accurate. Rather, there has been a belief that the uncertainty of the wave equation is a true feature of light and matter.
However, after deconstructing all physical phenomena to mathematical symbols and abstractions, what one needs to do is to construct the physical phenomena back to non-abstract, visualizable, entities. Pictures one’s five-year-old kid, or one’s grandma could understand. Before this, one should be aware that one doesn't really know what one is talking about.
Well, here is my picture to grandma:

The yellow spheres are the elementary particles, or dots, moving in pairs in double-helical orbitals in matter. The yellow curves are the actual paths in which these dots move at the speed of light in matter. And while this model only depicts ten dots out of an unimaginable number, and the curving is wildly exaggerated, there is no other ‘lies to children’, or simplifications in it.
The above image doesn’t describe all particles, such as electrons. However, the shape of these, I have already described in previous posts.
So, how do I know the structure of the matter to be just like that which I show above? Well, it’s all about gravity. I didn’t even realize the magnitude of the idea when writing my last blog post, but had the first idea of it, when I introduced the post on my Facebook page. In there I said: “What these interactions are, are a form of quantum gravity, but with the arrow of correlation directly pointing towards gravity causing quantum effects and not the other way around.”
Only after a while I realized that this is a crucial realization. It is gravity that forms the double-helical toroidal orbital. But not this abstract mathematical concept of gravity, as introduced by Newton, but the relativistic concept of gravity, as understood by Einstein. Well, even Einstein wasn’t able to see through some of the abstractions, but he was very close to understanding gravity down to the subatomic level.
So, what is gravity at the subatomic level? You might remember that I’ve mentioned that a single dot doesn’t have rest mass, but only relativistic mass. This is seen in light being comprised of individual dots, with no rest mass. So, what is rest mass? In short, it is the pairing of dots. In charged particles the concept is more difficult to see, but in non-charged molecular orbitals, this pairing is as clear as day. In the molecular orbital, this pairing means that the dots move in such an orbital that right next to them, there is another dot moving along the same orbital, but with a distance of half an orbital, despite the two dots physically touching.
This orbital is the famous toroidal double-helical orbital. In practice it means that the movement of the dots comprise of two elements: a linear element, which is almost at the speed of light, and a rotational element, which is significantly slower than the linear element. As these speeds are always orthogonal to each other, the follow the Pythagorean law: the sum of their squares is the square of the speed of light. Or more specifically, the linear and rotational components are really just a mathematical trick, and the movement is really just a helical toroidal movement, where each dot always travels at the speed of light.
And what does all have to do with gravity? Well, the dots would move in a linear path, just like light in a vacuum, but they cannot, because they are interacting with other dots. The neighboring dots are blocking this linear movement. But if the dots cannot move linearly, what do they do? Well, they begin rotating around one another. This means that the distance between two dots is exactly zero, but the distance between their centers is the diameter of a single dot. This means that the radius of this orbit is the radius of a single dot.
And how fast does the dot orbit this tiny circular orbital? In the time it takes to go around the larger toroidal orbital twice. Why twice? Because after a single turn of the toroidal orbital, the dot doesn’t go back to its original location, but to where its pair is at. So directly in contact with the dot that was in the location where the orbited dot started, but a center-to-center distance of one dot. To get back to its original location, it needs a second turn of the toroidal orbital.
But now you might ask, why can the dot remain in this rotating orbital in the first place? Why doesn’t the orbital just unravel? The answer is a word familiar to people reading popular science: entanglement. But just like many other mathematical truths, without connection to real life, familiar terms become mystical and otherworldly. Entanglement just means that there are two almost identical orbitals occupying the same toroidal surface.
In the image below I show a segment of this toroidal surface with two different colored orbitals: in in purple and one in yellow. The distance between these two orbitals is always 90°. As a single orbital occupies two halves of a toroidal surface, you can see the toroidal segment being split into four segments by the two orbitals.
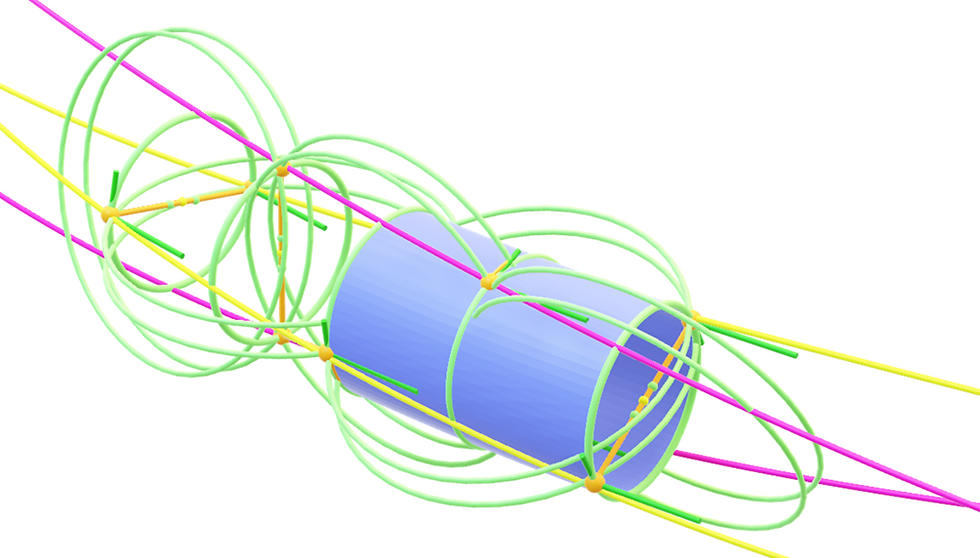
But as you can see from above, there’s so much more to this geometry. As in my previous post, but now in a more elaborate form, you see vectors separating the two sides of a single orbital, but you also see vectors connecting the two orbitals. The length of these vectors is always the same. Or more specifically, there really aren’t any vectors, but if I tried to illustrate the phenomenon with large spheres, as in my initial image, you couldn’t really see anything else. So I’m using a mathematical trick and illustrate the dots with vectors. And I can do that very well, if I just follow the rules, and hopefully go back to showing the dots after doing these mathematical tricks.
Unlike in my last post, by extending the orbital to more dots I see that there are more than one large ring surrounding the intraorbital vector, or the vector that connects the orbital with itself. If the curvature of the orbital was zero, there would just be one ring. But as soon as there is curvature, this causes the formation of two rings symmetrically on either side of the center point of the intraorbital vector. One of the rings defines and interorbital vector (or a vector connecting the two orbitals) to one side of the intraorbital vector and the other ring defines and interorbital vector to the opposite side. And almost magically, you have just defined a double-helical toroidal orbital.
But now that we’ve done our mathematical tricks, lets zoom out and reduce the number of mathematical abstractions. First, we’ll lose the toroidal surface, because it doesn’t really exist in real life. Second, we make the double-helical orbitals the same color just to allow one to focus on other aspects. Below is exactly the same relations, but less help to explain what everything means.

But even now, we still have the circles, that don’t really exist in the structure. So, we can ditch the circles and are only left with tiny spheres to mark the centers of the dots and vectors of equal length to define their distance. But we still retain the double-helical toroidal orbital to mark the path of the movement of the dots.

And finally, we can expand the spheres marking the centers of the dots to the size of the dot. Now we don’t need the vectors any longer.

This is how you use mathematics to test physical principles and make abstractions that you can convert to equations. However, ultimately you must be able to go back to the dots moving at the speed of light and the paths of their movement. If you stop before this point, you are left with a magical notion of how the world works. A world where particles are probability clouds with no defined location, speed or probably even a vector of movement. In this magical world, a collection of dots is mistaken for a particle with mystical properties, such as attraction without physical contact.
So, if what I propose is the first non-magical interpretation of the world, what is the most commonly held philosophical understanding of the world at the moment? It is a concept called physicalism. Wikipedia states:
The terms "physicalism" and "materialism" are often used interchangeably but can be distinguished based on their philosophical implications. Physicalism encompasses: matter, but also energy, physical laws, space, time, structure, physical processes, information, state, and forces, among other things, as described by physics and other sciences, as part of the physical in a monistic sense.
This is a very convoluted way of saying that world cannot be materialistic, because there are also true physical phenomena that have no matter. But really physicalism is a way of skirting the problem of what energy most fundamentally is. Again, according to Wikipedia:
In physics, energy is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat and light.
From where I’m looking, this explanation is to some extent animistic. In current physicalist approach, energy is an abstract intangible essence of all being, which cannot be reduced to an understandable physical entity. And the way scientific publishing has worked up to this point, it was almost impossible to break this line of thought. You see, I have been expressly told that my approach doesn’t follow the scientific method. I’ve talked about this in my previous posts. Again, according to Wikipedia:
The scientific method is an empirical method for acquiring knowledge that has characterized the development of science since at least the 17th century. It involves careful observation, applying rigorous skepticism about what is observed, given that cognitive assumptions can distort how one interprets the observation. It involves formulating hypotheses, via induction, based on such observations; the testability of hypotheses, experimental and the measurement-based statistical testing of deductions drawn from the hypotheses; and refinement (or elimination) of the hypotheses based on the experimental findings.
However, there is an unwritten postulate in physics. An that postulate is the ab-initio state of the wave equation, or the idea that quantum effect are not an emergent property of something more fundamental that do not follow the wave equation. You need to begin with the wave equation and come up with experiments that test your hypothesis. But if you don’t begin with the wave equation, you first need to have experimental evidence to fit the new equations into, but the problem is with the energy scale required for experimental verification of string theory is beyond what we have at our disposal at the moment, or will ever have. Except, we are looking at the problem at a ridiculous perspective. You see, particle physics has relied on particles colliders to offer direct evidence of subatomic particles. An this has led to the idea that you cannot deduce the properties of subatomic particles without separating them from each other with high-energy collisions. But to separate any subatomic particles into massless particles (or just light), the amount of energy you would need, cannot be replicated on earth.
So, the only option is to ditch the conventional scientific method. I know this sounds heretical, but if we already know that the amount of energy required to prove string theory experimentally with particle colliders is too high, we have to work with hypotheses. And the problem with hypotheses is that they are almost by nature simplifications of true phenomena. And you are bound to make serious mistakes. This I know, as my path to this point hasn’t been straightforward and without errors. But the fact of the matter is that the only way to figure out the truth is to follow logic wherever it leads and trust that the world is a logical place. But what happened once the scientific consensus rejected Einstein’s idea that “God doesn’t play dice”, was that people lost their belief that the world is an inherently logical place. Or more precisely, they believe it up to the point of the level of quantum interactions, and then raised their hands and say: “this is just mathematics”. But it’s never just mathematics. If the mathematics of physical phenomena are not connected to real life, then there is something wrong with the postulates.
But mathematics isn’t the problem. The problem is the childish philosophy that is attached to partial understanding of physical phenomena. But the best way to address this problem is to solve the problem mathematically and not to engage in philosophical squabbling. But you must wait until my next post until you’ll be seeing more equations.




Comments