Kau Through the Looking Glass
- Kalle Lintinen
- Dec 13, 2024
- 3 min read
In my last post “Known Knowns”, I presented the simplest unit sphere of reflection and presented the geometrical logic behind all of the nodes in the shape. In the post I promised that I wouldn’t post anything until I have the equations that allow me to present a hinged sphere of reflection:
“Perhaps this is my goal: only post something If I’m able to present an accurate unit sphere with a hinge angle of ten degrees. And before I can, I’ll refrain from posting.”
However, in today’s post I’m going to break my promise. The reason is quite philosophical and relates to reflection where the reflected particle goes through the looking glass. Just like Alice, the elementary particle of energy (kau/dot) goes through the reflective surface. And when this happens, ordinary logic of reflection no longer holds. You see, with reflection of light, the reflected shape is by definition a mirror image of the original. In chemistry this is called chirality. However, when the reflection doesn’t reverse the main path of the kau, the reflection becomes achiral, and the reflected shape is no longer a chiral mirror image. Rather, the reflection is more like the pinhole ‘lensing’ of a camera obscura.
So, how does this affect the sphere of reflection? Well, it indirectly shows that my old unit sphere of reflection was too big. Or more specifically, I had rammed two unit spheres into one, which caused a lot of problems. The true unit sphere of reflection is simpler and consists only of four kaus, each residing on the surface of the sphere. Here is the basic shape with a hinge angle of zero:
This slightly simpler than before shape is the unit sphere of reflection and not the shape of the Known Knowns -post. That shape wasn’t wrong as such but ended up being very misleading. So, let’s break down the above shape. The purple horizontal rods are the grazing paths. I’ve also drawn how the grazing paths extend to neighboring unit spheres, but these rods aren’t actually part of the unit sphere in hand. All of these four purple rods are associated with a single yellow kau, located at the end of the yellow grazing rods. Two of these kaus are connected to a blue (diagonal) reflection rod with grazing paths. The blue reflection rods of the other two yellow kaus are located in the neighboring unit spheres. I’ve also drawn a green rod to mark the path between the centers of two yellow grazing connection rods. Next, I’ve added red rods around the blue reflection connection rods. This rod, which is not the same length as the purple grazing rod when the hinge angle is above zero, is a geometrical aid that allows me to see that the purple grazing rod can be replicated elsewhere in the shape as well, which in turn means that the red geometrical aid can be replicated as well.
I’m sure all of this is just complicating thing for you, dear readers, but rest assured that these should allow me to define the geometry of reflection perfectly.
And what does reflection look like using this unit sphere?
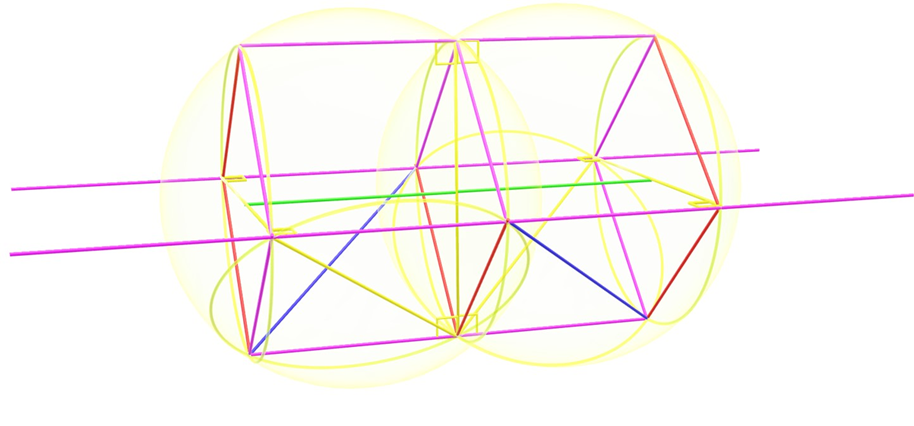
Focus first on the yellow vertical grazing rod. There is a symmetrical kite-shaped quadrilateral. And on either side of the kite there are unit spheres that are otherwise identical, but the right side is the left side rotated 180 degrees around the central vertical rod. And you can duplicate this shape by rotating the pair of unit spheres around the horizontal yellow rod:
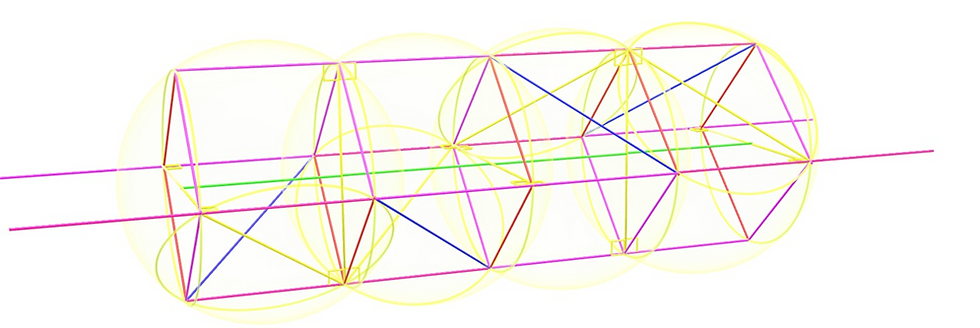
And if you look closely, you see that when four of these unit spheres are connected together, you can just add a duplicate of this quartet in front of the first quartet to form an octet, as the double-reflection has turned the shape to its original configuration.
This looks extremely convincing. However, I still need to convert the shape into equations to be 100 % sure that it’s correct. So watch this space…




Comments