For a while, I’ve been thinking about names for my Theory of Everything. To some extent I could still call it string theory, but I think the name has a lot of baggage. Especially the assumption of extra dimensions. For some time, I’ve just called it the “Dot Theory”, based on the elementary particles of energy. However, I’ve always been a bit reluctant in removing the connection to string theory altogether, because it is still based on the same general idea.
But now that I realized that the string of dots isn’t ripped when one string entangles with another string, I have a clear shape, which is very much like a string, but not quite. This new shape is a rope ladder. Or more specifically two ropes connected with ‘step rods’ at constant intervals. Another name for this is Jacob's ladder. So, at least for now, I call my theory Jacob’s Ladder Theory.
So, does this name have any practical implications? Well, sort of. It emphasizes the fact that you can define the connections between dots with three vectors for each dot. And just considering this, it opens new trains of thought. First of all, I know that the true shape of entangled strings of dots looks like this:
However, this shape does not have sufficient abstractions to do proper mathematics. You see, abstraction is the ‘sin’ of mathematics. You take something true, but a difficult to understand and chip away all of the useless things for mathematical analysis, and you’re left with something that isn’t exactly true, but much easier to handle. So, I can take the image above with spherical dots, and to make things easier for me mathematically, I can pretend that the spheres aren’t spheres, but really cylinders, like this:
The above shape isn’t as true as the one with the spheres, but you can use it much better for mathematics. You see, just from the spheres you can’t really deduce how the vectors that define the Jacob’s ladder are located. So, you have to reduce the sphere to a shape that reveals the vectors. What I’m really interested are two circles that are on the surface of the sphere. The easiest way to draw such a shape is with a cylinder, so this is what I use for the Blender image. However, I’m not really interested in cylinders, but in cones. You see, with two cones touching at the center, you can depict both the center of the sphere and the two circles of refraction on the surface of the sphere. The problem is that while I can draw the shape that I’m looking for in Blender (as seen below), I don’t yet know how to make an array like the one above with this double-cones.
However, while it was very hard to find the vectors from the spheres in the first (true) image, it is already much clearer to see the vectors with the cylinders and pretty much obvious with the cones. Thus, while the sphere is the true shape, we need to reduce it into two connected cones to observe their interactions.
Now that we have the double-helical orbital described with cones, it is easy to forget that this is just a mathematical trick. Looking at the edges of two cones balancing just so that a vector can be drawn from the tip of one cone to the tip of the adjacent cone, it seems like there’s some magic keeping the cones connected this way. However, there’s no magic. There are just two spheres touching each other in a very solid manner. The only reason the angle is they way it is, is because you don’t see the two strings of dots twisting around each other, forming these angles.
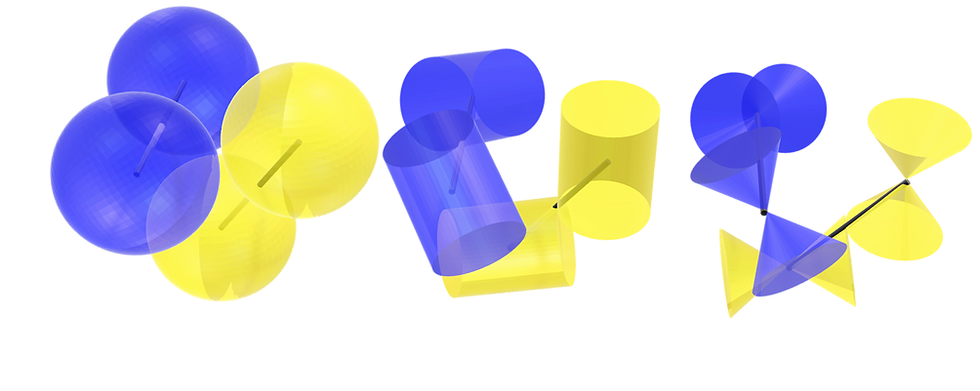
While there’s no new mathematics in here yet, I think I need to include this at least in the supplementary information of the Theory of Everything manuscript.
However, I’m also tempted to what the Mark Watney character did in the Martian:
The only thing is that this will take more time. But I’m in no hurry. At least I’ll see how easy or difficult this will be.
留言