I Finally Bent Water!

I’ve been relatively quiet in the posting front these past few weeks. But this hasn’t been because I haven’t been doing anything. Pretty much the opposite. I’ve finally found a way to describe reflective gravity with proper mathematics. But it has taken quite a long time for me to pass from a stage of and then a miracle occurs, to proper equations. But today’s the day.

But before I go to the final mathematics, lets go back to basics.

For a long time, I wished I could tackle the Theory of Everything in one paper, but only when I realized I had to pick a single topic that actually related to my experimental work, did I start to get a proper mathematical handle on things. At first, I took the easy step and described how monolignols must be pressed into helices after biosynthesis inside plant cells just by being pressed by the surrounding water and other biomolecules in the nearly solid-like aqueous environment within the plant cells. As no molecules carrying the monolignol through the cell membrane of plants have been found (despite considerable effort to find one), one must assume that monolignols must move as clusters. Except these clusters aren’t random aggregates, but rather as very clearly defined helical toruses.

These helical toruses of monolignols are the backbone of my paper. These explain the existence of the primary structure of lignin, which are a helical lattice of these toruses, entangled into double helices and biopolymerized into lignin only after the entanglement. As you can see from the Wikipedia page on biopolymers, a double helix is a very common shape for them.

So, what do monolignols or lignin have to do with reflective gravity? Well, in the paper I propose that entangled double helices are not just a property of biopolymers, but of all gaseous and liquid molecules. When molecules move in liquids, the motion cannot be truly random, but the molecules (such as water) must be helical arrays, moving as helical waves. The key realization I had a while ago was that there must always be two arrays winding around each other, but where the direction of motion of the molecules in one helix is opposite to the other. This way the molecules in the neighboring helices can prevent each other from fully unraveling. Well, actually explaining why this is, is quite complicated, but I’ll give it a go.

It appears that the helical motion is split into unraveling and winding turns (or quarter-turns to be precise). When an entangled pair of array of molecules are bent into helical arcs, half of the molecules are on the inside bend of the arcs and half are on the outside. However, as these helices bend into a torus, there is also the inside and outside bend of the torus as well. And the curious thing is that depending on which side of the torus the molecules are at, at any given moment, they move according to two different sets of equations. Half of the time, the molecules are on the inside bend of the entangled helix are getting further away from the origin of the arc, or unraveling. And the other half of the time they are on the outside bend are getting closer to the origin of the arc, or winding.

Just as a teaser, here are plots of how the equations would show these entangled helices, if the minor radius of the water torus was not much larger that the radius of a single water molecule:

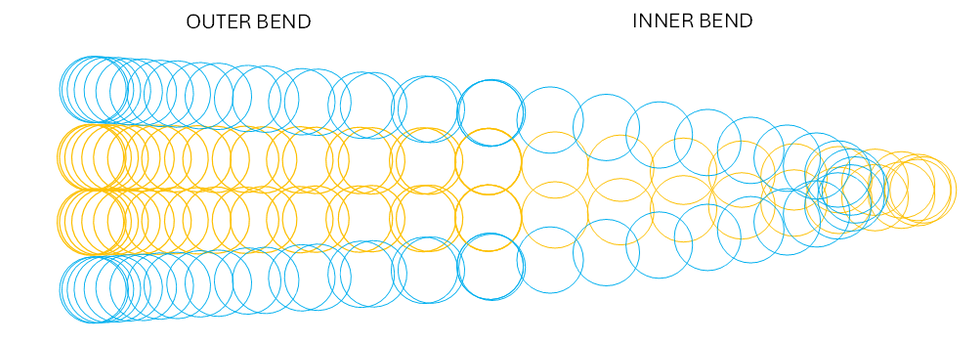
And here are the connection points between the helices of inner and outer bends:

The above zig-zag is what ultimately bends into a torus. In a sense, the individual helices ‘don’t see’ this higher-level bending. The bending is more or less an emergent phenomenon of entanglement.  Of course, to form the equations, nothing emerges from thin air. It took forever to figure the equations out. If I start counting from when I got the idea of toroidal monolignols, it has taken five years, four months, and if I start counting from the moment I realized there must be an elementary particle of energy it has still taken three years, eight months.

But now it’s ready! Or at least the first mathematical step. It will take some time still for everything to be sorted out, but if I get this published, it no longer has to be just me who’s going to try to solve this.