It wasn’t too many days ago that I posted that curves don’t exist. The reason for this was that it seemed that there is a discreet number of impacts, where the trajectory of elementary particles of energy (dots) changes. While I don’t think this truth has changed, I’ve begun to question the instantaneity of the impact. Rather, it seems that as two dots impact, they travel at least for some time along their surfaces.
So, what does this look like? That I don’t know. I just do know that if there is a pair of dots, they can only move in a straight line and touch at the end, if the two straight lines are parallel. This means that such a pair could be reflected, but only forming a circle of dots, However, to form a saint Hannes knot, they either need to move in a curved path, or then they cannot touch each other after reflection. If we rule out the pair not touching, this will only leave the option that the pair of dots rotates as it’s moving.
I have to own up, that the angled equations that I showed before were a bit off. I had forgotten a term for the parametric equations for the z axis. While losing it didn’t affect the main idea of the post, forgetting the term made the equations impossible. Here are the corrected equations, which might be fully correct, or not:
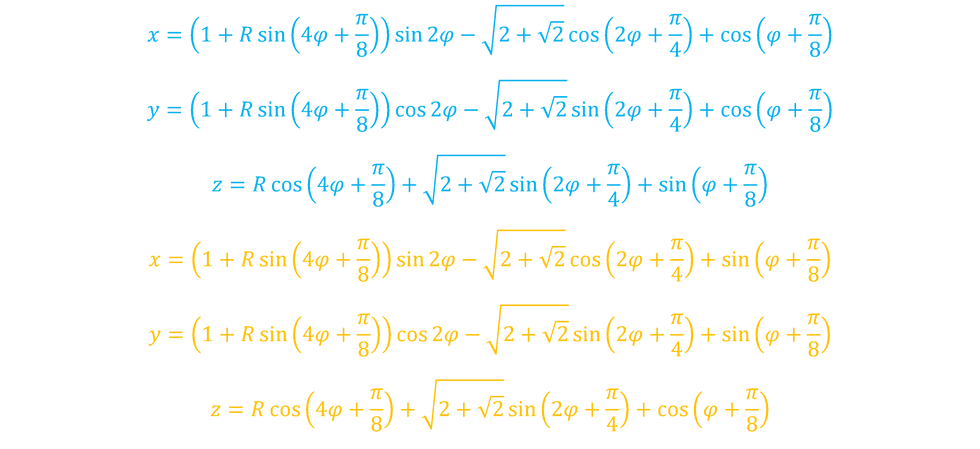
And here are the x-z and y-z projections of the knot:
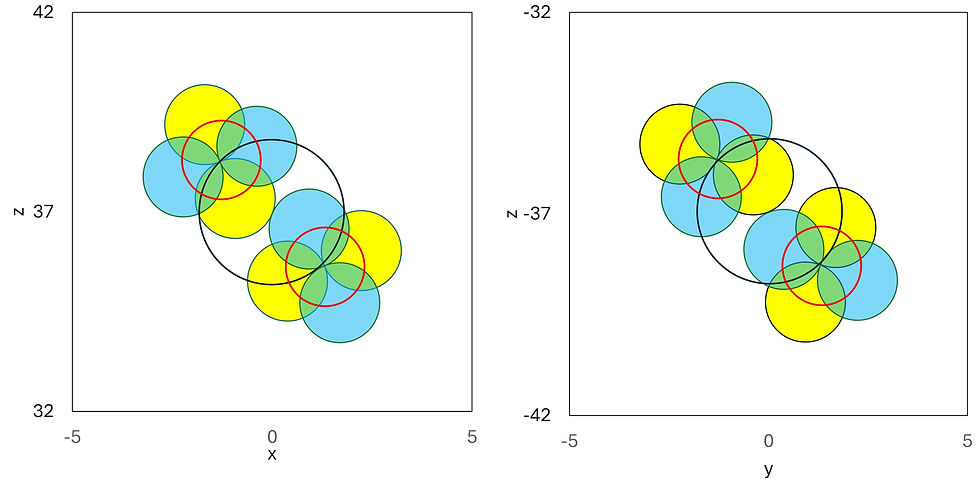
The black larger circle depicts the reflections with a normalized radius of √(2+√2).
I was about to say that in this ‘one-off impact’, there is no rotation at the point of impact. But now that I look at the image, that’s exactly what the equation implies. I.e. the impact here isn’t instantaneous either.
And the smaller red circle depicts the reflections with a normalized radius of one, where all of the (same-colored) pairs of dots rotate around each other. And where the impact isn’t instantaneous.
My intuition says that after the long, curved, impact, the dots do also fly a while in a straight path before the next impact.
But these are still early days. I’m bound to find a bunch of errors in my logic. However, I’m making progress and that’s what matters.
Commentaires