Building the Higgs Boson One Vector at a Time

In my last post I made the statement that I should be able to come up with the shape of the Higgs boson, just using linear algebra and more specifically vectors. I also said that the tools at my disposal are quite clunky. However, sometimes clunky tools force you to think more deeply about the underlying mathematics, because you can’t just brute force yourself out of problems.

This time the good thing is that I already have much of the geometry sorted out, which should mean that the mathematics just comes from expressing the geometry in a more systematic way. In my last post I showed this image:

It almost correctly illustrates the principles involved in the curving of an entangled double helix of dots. Except it assumes that the elementary particles of energy (dots) of one helix rip apart, making a zig-zag pattern of connections. I no longer think that this is the case, at least at equilibrium. This might be a feature of collisions, but for now we can just ignore this.

So, if I take the basic concepts of the image above and apply my current understanding of the geometry of the entangled state and use the cone of refraction to describe the geometric relations, we get this image:

Or viewed from the side:

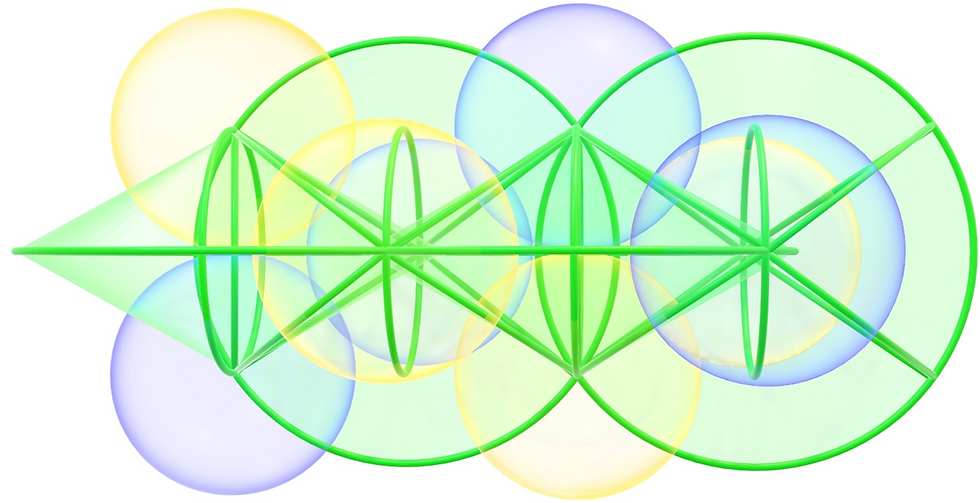
The good thing about this image is that it’s extremely accurate. The bad things are that a) it’s cluttered with so much information that it’s difficult to comprehend with a single viewing and b) it portrays a case where there is no refraction. In this case the neighboring cones of refraction touch. Why I started with this case is that it’s infinitely easier to visualize.

And another good thing about this image is that you can cheat a bit. Without touching the geometry, you can just remove a couple of vectors and recolor other vectors and you get this:

I call this pseudo-twisting. It illustrates twisting in the case where the twist is zero.

The next step is to formulate the equations that describe this. I already have the equations from the time I thought the helices rip apart. I should be able to relatively easily correct the to match this shape.

I have a feeling that with these equations, I should be able to describe the Higgs boson one vector at a time. But I’m not yet at that point, despite the title of this post.