An Origami Teaser
- Kalle Lintinen
- Jun 6, 2023
- 3 min read
In my last post I gave a sneak preview of the mathematics of the tangling of a double helix of dots into matter (hydrogen), with a picture of rather complex-looking equations.
In this post I don’t show any of the equations, but I reveal a bit of the logic behind them. At first I had just the idea that the dots are arranged in semi-rigid rods that for some reason twist. The initial orientation for the dots (depicted below as hollo circles) was as simple as possible, with the alignment of the dots following the x, y and z axes, like this:

Then I got the idea that not all of the dots that look connected are connected only with three neighboring dots, instead of all four dots. The only problem was that visualizing this concept with spheres was near impossible. But if instead of spheres, I visualized the connections with the spheres. And only the spheres that touch. The three touching spheres would form an equilateral triangles with the points of the triangle at the centers of the spheres. To cut a long story short, I also rotated the series of six spheres so that the first triangle would be drawn om the x-y, plane with the first line being a vector with a length of 1 along the x-axis. Looking at it from three directions (xy, yz and xz) they look like this:
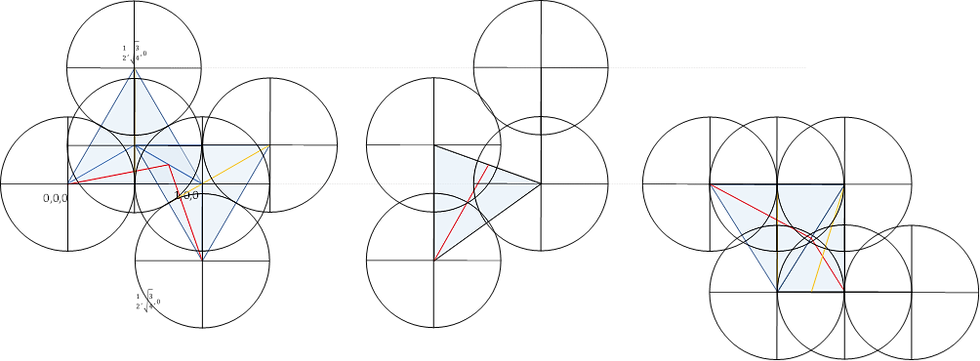
This is kind of better, but having the circles also there just makes things confusing, so I ditched those. They didn’t add any mathematical information to the scheme. So without the circles, the triangles look like this:
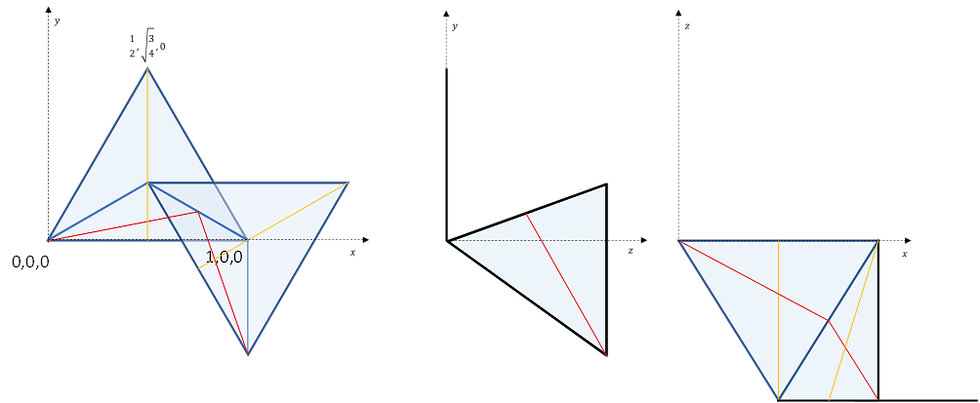
Looking quite abstract in comparison, but much, much clearer. I also drew ‘hinges’ to the triangles, because that is how they ‘open’. Or more specifically, if the collection of spheres was entirely linear, you could add equilateral triangles to the two open sides and you would have a collection of equilateral triangular pyramids.
However, just like with light, these dots encounter refraction and begin moving in a helical trajectory. But this refraction is not from the surrounding environment, but from the other dots in the same orbital. So, I invented a word for this phenomenon: “orbital refraction”.
So above you see the six dots (spheres) reduced to four triangles. What would it look like if there were many more dots? Well, let’s look at the case of 14 dots. While the folded shape looks pretty odd, this is still a linear arrangement of dots, just like in the first picture

Ok, then what? Then I need to start increasing the angle between the triangular sheets from atan√8 (or roughly 70.53°) to a bit higher to see how this origami begins to twist and arc. And for this, I need to describe the first triangle as three vectors and derive all subsequent triangles from simple rules, using trigonometry.
The fun thing is that after I’ve illustrated the 3D structure of the origami, I can see the structure from which the complicated looking structure has been folded from. And it’s dead simple. Just make a 2 D strip of triangles and form creases by folding pairs of triangles in half, like this:
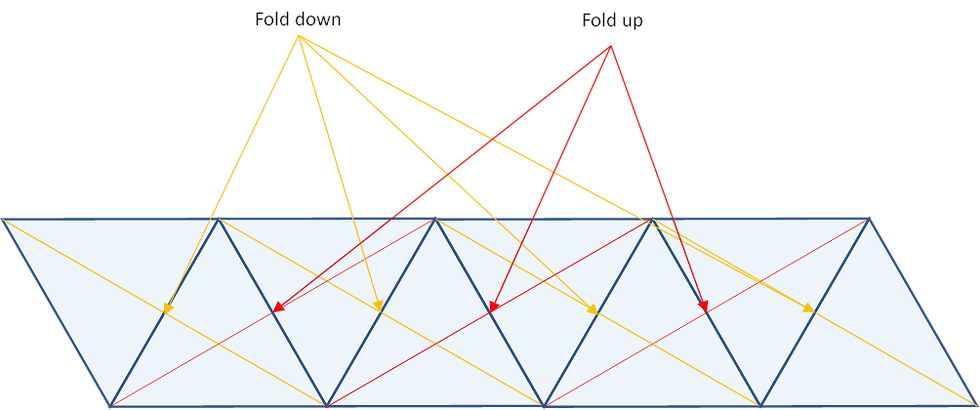
And just to bring the abstract mathematics back to real-life dots, here is how this 2D strip of triangles looks like in actual dots:
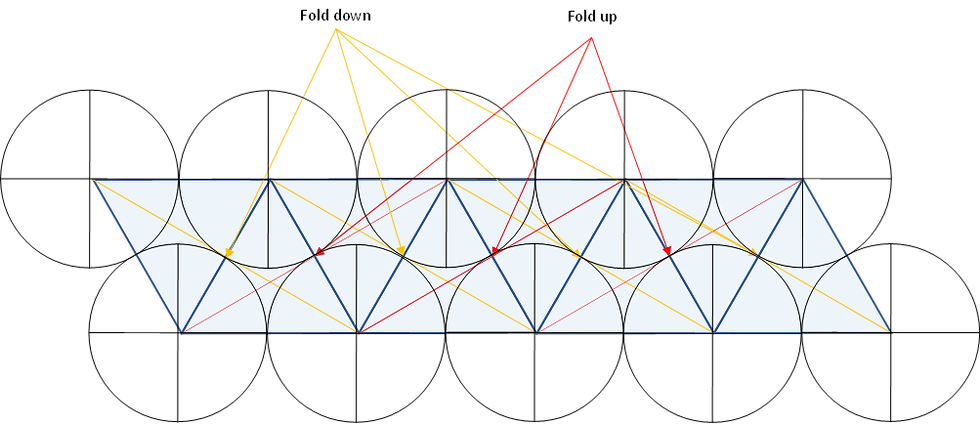
I’m making good progress, but won’t be able to show the calculations yet. This is because everything has to be correct for me to be able to put the data into Excel and plot them. 95 % right isn't good enough.
And boy is this taxing to the brain. I can only do this in small chunks and then I just need to take a break. It’s all about vectors, matrices, cross products, algebra, trigonometry, topology and all sorts of concepts that soon turn into mush in your head, unless you find a clear way to present everything. This is exactly what I’m doing in this post. Taking the rather messy looking image from the last post and forcing a bit more order into it. This way I can more easily check where there are errors in my equations. And I always have errors. They are never correct on the first try.
But this is the joy of mathematics and science. You can immediately see whether you are on the right tracks, if things become logically consistent. With mathematics you can have perfect proofs. However, with science, at least up to now, you’ve always been a bit unsure, even after everything seems to add up. But it just might be that with this spring-string theory, one can finally make science as accurate as mathematics. At least that’s my hope.




Comments